ABSTRACT
This work addresses the general problem of resilient control of unknown stochastic linear time-invariant (LTI) systems in the presence of sensor attacks. Motivated by a vehicle cruise control application, this work considers a first order system with multiple measurements, of which a bounded subset may be corrupted.
A frequency-domain-designed resilient parameter-invariant controller is introduced that simultaneously minimizes the effect of corrupted sensors, while maintaining a desired closed-loop performance, invariant to unknown model parameters. Simulated results illustrate that the resilient parameter-invariant controller is capable of stabilizing unknown state disturbances and can perform state trajectory tracking.
PROBLEM FORMULATION
This section introduces a resilient control problem for a system with unknown LTI-Gaussian dynamics and (potentially) corrupted measurements. Specifically, we consider an LTI system with a single state that evolves according to
x (k + 1) = ax (k) + bu (k) + w (k)
y (k) = cx (k) + v (k) + d (k)
where:
_ { x; u 2 R, are the state and control input, respectively;
_ { a; b 2 R are the state dynamic and control input gains;
_ { y; c; d 2 RN, are the measurements, state measurement gain, and corruption, respectively;
_ { w 2 R and v 2 RN are uncorrelated i.i.d. Gaussian process noise and measurement noise with central moments1:
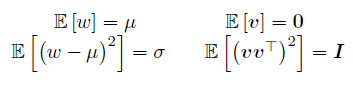
MAIN CONTRIBUTIONS
By extensively employing the notation and denitions introduced in the appendix, the main contributions of this work are summarized in the following propositions:


RESILIENT PARAMETER-INVARIANT CONTROLLER DESIGN
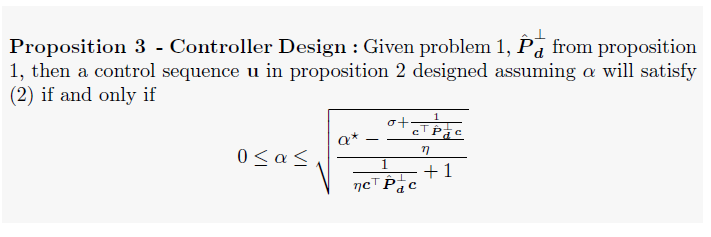
From the previous section, it is clear that the performance of the resilient state estimator affects the controller. Since it is a primary concern to secure the measurements against malicious attacks, and a secondary concern to maximize the performance with respect to the environmental unknowns, we introduce the fol- lowing proposition to design the parameter-invariant controller convergence rate,
SIMULATION RESULTS
This section provides a qualitative evaluation of the resilient parameter-invariant controller. This evaluation is presented in two subsections. The following subsection presents disturbance rejection results considering first order systems, both unstable and stable, when sensor corruption is both present and absent. The final subsection presents a simulated cruise control scenario for robotic platforms.
Fig. 1 presents the results for a stable system with no sensor attacks. In Fig. 1, we simulate a state disturbance injection (beyond the process noise) occurring every 30 time steps. It is clear that the controller is capable of stabilizing the system, and achieves the performance bound on the norm of the state; however, we note that despite no attacks being present in this simulation it is assumed that some of the sensor measurements are corrupted at most time steps.
A unstable system with no sensor attacks is considered in Fig. 3. Similar to the results for the stable system, here we observe that resilient parameter- invariant controller stabilizes the system with respect to unknown disturbances, and has a response very similar to the stable system results in Fig. 1.
The cruise controller performance in the presence of a sensor attack on sensor three is illustrated in Fig. 6. Here we observe, and consistent with previous observations, that when attacked, the measurement of sensor three is accepted less often. In this case, sensor one (known to be more noisy) is selected more often. This results in the need for, on a average, a more aggressive control law to meet the performance criteria.
DISCUSSION AND FUTURE WORK
This work addresses the problem of resilient control of unknown first-order stochastic LTI systems in the presence of sensor attacks. A resilient sensor fusion strategy is introduced that minimizes the likelihood of a corrupted sensor being trusted. A time-series concatenation of secure estimates is utilized in cooperation with a desired state trajectory and previous control inputs to design a mean-stabilizing finite-horizon control sequence, invariant to the unknown system parameters.
The parameter-invariant controller is designed using a frequency domain representation of an equivalent time-series representation of the system inputs to system outputs, thus allowing the design of a mean-stabilizing controller. Simulated results illustrate that the resilient parameter-invariant controller is capable of stabilizing unknown state disturbances and can perform state trajectory tracking.
Future work on this topic includes the extension of the scalar results in this paper to multi-dimensional systems with known dynamical structures but unknown parameters. A limiting factor in the application of the resilient parameter- invariant controller is the requirement (at this time) that the system-to-be- controlled behave as a linear first order system. While most stable systems can (at some time scale) be approximated by a first order system, this approximation can be very poor.
As future work, we plan to evaluate the proposed control strategy on various experimental platforms to determine the robustness of the parameter-invariant control with respect to the design dependency on a first-order linear system. Additionally, further insight is needed to investigate a method to reduce (or remove) the lag and to quantify its behavior in terms of the underlying system and design parameters. Experimentation of the resilient parameter-invariant controller is planned on a robotic platform as a potentially cooperative approach with model-based approaches which assume knowledge of model parameters.
Source: University of Pennsylvania
Authors: James Weimer | Nicola Bezzo | Miroslav Pajic | George J. Pappas | Oleg Sokolsky | Insup Lee


