ABSTRACT
The on-demand approach, where systems are assembled from components by lay users, has seen success in the consumer electronics industry. Currently, there is growing demand for on-demand capabilities in medical systems so caregivers can create larger medical systems from smaller medical devices. Unlike consumer electronics, medical systems pose challenges for the on-demand approach due to attributes such as device complexity, device variability and safety requirements.
In this paper, we propose a formal specification language for on-demand (medical) systems. Our approach is based on the formalism of Modal I/O Automata, which allows system designers to express complex device requirements and can be used to reason about safety and liveness properties of on-demand medical systems directly from their specifications. We illustrate the applicability of our approach through a case study of a closed-loop patient controlled analgesia system.
MOTIVATING EXAMPLE
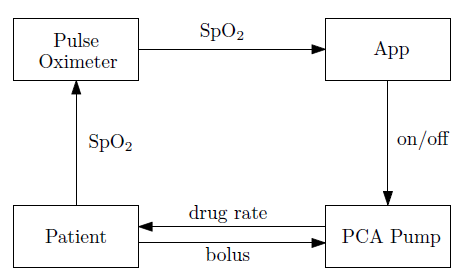
Fig. 1: A closed-loop PCA system.
As shown in Figure 1, the system consists of four components: a pulse oximeter, an app, a PCA infusion pump and a patient. The system operates in a closed-lo op fashion: the pulse oximeter keeps monitoring the patient’s SpO2 value (measure of blood oxygenation), and the app controls the PCA pump based on the SpO2 value read from the pulse oximeter (the app would stop the pump if the detected SpO2 value is lower than 95).
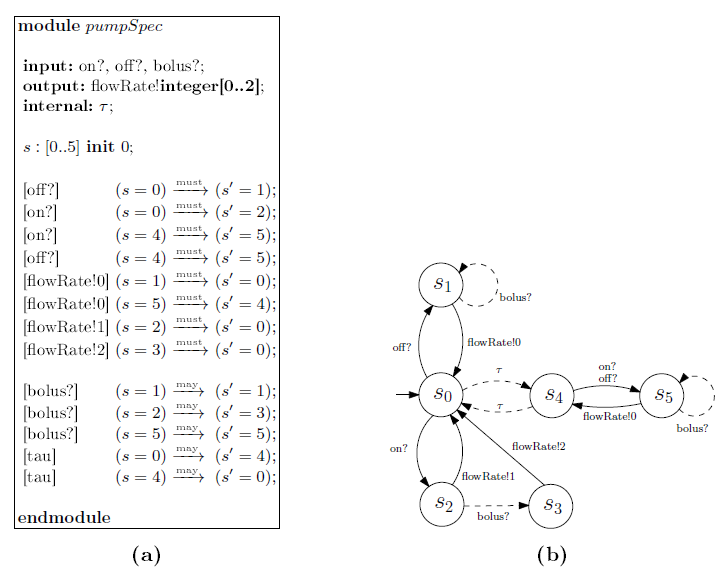
Figure 2 illustrates the behavior of three different types of PCA pumps as state machines. Figure 2a represents a simple infusion pump that infuses while it receives the on signal. Technically speaking, the pump of Figure 2a is not a PCA pump because it doesn’t provide any mechanism for the patient to request a bolus.
Figure 2b represents a PCA pump that will infuse at a rate of 1 while it receives the on signal and it will infuse at a rate of 2 when the patient requests a bolus, even if it is receiving the off. Finally, Figure 2c represents an even more complex PCA pump. This pump will autonomously disable itself under a number of conditions in order to mitigate several hazards associated with infusion pumps.
A SPECIFICATION LANGUAGE FOR ON-DEMAND SYSTEMS

Fig. 3: An example module specification.
Figure 3 shows an example module M1 described in our proposed specification language. The description is split into four parts, defining actions, state variables, as well as must and may transitions of the module. The module M1 has two input actions: “a?integer[1..2]” that receives a integer value within the range f1; 2g via channel “a”, and “b?” that receives an input via channel “b” (the message is omitted). The module may send an output through action “c!”, and has a single internal action ⊤.
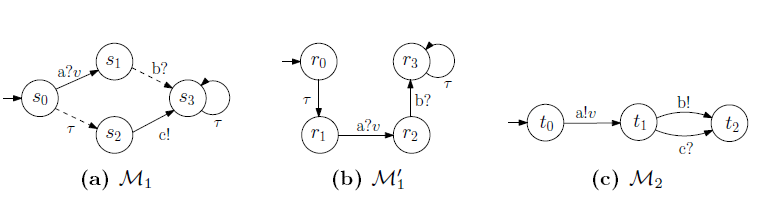
Fig. 4: Three example MIOAs.
The module M1 described in Figure 3 maps to the MIOA M1 shown in Figure 4a. There are four states fs0; s1; s2; s3 g in M1, each of which maps to a valuation of variable s = i for i 2 f0; : : : ; 3g in M1. The initial state of M1 is s0, indicated by an incoming arrow in Figure 4a. The must transitions are drawn in solid arrows, while the may transitions are drawn in dashed arrows.
CASE STUDY
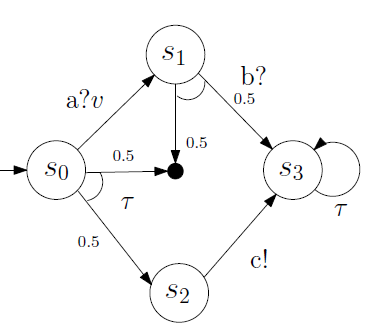
Fig. 6: Translation of the MIOA in Figure 4a for PRISM.
For example, Figure 6 shows the probabilistic translation of the MIOA in Figure 4a; the may transition from s0 to s2 now becomes a transition with probability 0.5 (the black dot is the sink state). If PRISM verifies that certain property is true with probability 1, then the property “must” be satisfied by the on-demand medical system; and if the verification result is a real value p such that 0 < p < 1, then the system “may” satisfy the property.
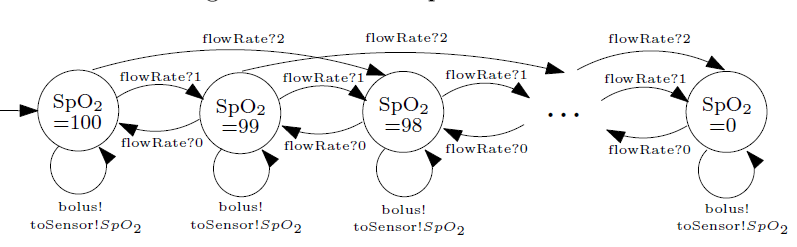
Fig. 8: MIOA for the patient dynamics.
As shown in Figure 8, each state of the MIOA for the patient model represents a single SpO2 value, ranging from 0 to 100. With an initial value of 100, the patient’s SpO2 measurement decreases by 1 or 2 upon receiving drug from the PCA pump at a normal infusion rate (“FlowRate?1”) or a bolus rate (“FlowRate?2”), respectively. On the other hand, the SpO2 value increases by 1 if the PCA pump stops (“FlowRate?0”), modeling the restoration of the patient’s vital sign as the drug concentration reduces.
Figure 10a describes the specification for the PCA pump, which should be provided by the app developers, and Figure 10b shows the corresponding MIOA. Under this specification, if the pump is enabled by the “on?” command from the app, then it can deliver drug to the patient at a normal infusion rate “FlowRate!1”; however, if it is disabled by the “o”?” command, then no drug will be delivered (“FlowRate!0”). Some pump may allow receiving “bolus?” request from the pa- tient, which are described as “may” transitions in the specification (dashed lines in Figure 10b).
CONCLUSION & DISCUSSION
In this paper we have described an approach to specify on-demand systems and applied that approach to an example application from the medical domain. This approach uses a specification language with the semantics of MIOA. We showed that weak modal refinement can be used to check the compatibility between app requirements and device capabilites by proving that weak modal refinement preserves both safety and liveness properties. This enables medical systems developers to express complex medical device behavioral requirements, explicitly specify allowed variability and reason about the behavior of on-demand systems a priori.
While we provided a case study as a proof-of-concept for the approach, there are many open questions concerning the engineering, safety and application of on-demand medical systems in a critical care setting. First we note that there are several areas where our proposed specification language and associated semantics would need to be extended to make the approach more applicable to real medical systems. For example, the action labels in our language are only tagged with simple data-types. Often, medical device actions relate directly to an interaction with the physical world (e.g., an infusion pump infusing a drug).
It would be useful if action labels could also be tagged with physical types which would denote the physical interaction of the action. Furthermore, our approach only supports reasoning about discrete time systems. Real medical devices exhibit continuous time behavior, and the ability to capture real-time behavior is critical if we want to apply our approach to real medical systems. For example, the on-demand medical systems described all rely on `timeout’ behavior in the medical devices to guarantee system safety in the presence of inter-device communications failures.
Additionally, many medical devices exhibit continuous behavior in terms of their interactions with the patient. For example, infusion pumps deliver drugs continuously according to `trumpet’ curves. It is not known to what fidelity a specification will need to capture device behavior: Is continuous time plus discrete behavior enough, or is a fully hybrid specification required? The answer to this question will likely depend on the types of on- demand systems clinicians will want to employee.
Source: University of Pennsylvania
Authors: Andrew L. King | Lu Feng | Oleg Sokolsky | Insup Lee