ABSTRACT
Data-driven techniques are used in cyber-physical systems (CPS) for controlling autonomous vehicles, handling demand responses for energy management, and modeling human physiology for medical devices. These data-driven techniques extract models from training data, where their performance is often analyzed with respect to random errors in the training data. However, if the training data is maliciously altered by attackers, the effect of these attacks on the learning algorithms underpinning data-driven CPS have yet to be considered.
In this paper, we analyze the resilience of classification algorithms to training data attacks. Specifically, a generic metric is proposed that is tailored to measure resilience of classification algorithms with respect to worst-case tampering of the training data. Using the metric, we show that traditional linear classification algorithms are resilient under restricted conditions. To overcome these limitations, we propose a linear classification algorithm with a majority constraint and prove that it is strictly more resilient than the traditional algorithms. Evaluations on both synthetic data and a real-world retrospective arrhythmia medical case-study show that the traditional algorithms are vulnerable to tampered training data, whereas the proposed algorithm is more resilient (as measured by worst-case tampering).
RELATED WORK
CPS Security
Though the security of learning systems for data-driven CPS has been an afterthought, the security of CPS has seen much effort in the past decade. A mathematical framework considering attacks on CPS is proposed. The necessary and sufficient conditions on CPS with a failure detector such that a stealthy attacker can destabilize the system are provided. State estimation for an electric power system is analyzed in assuming attackers know a partial model of the true system.
Learning with Errors
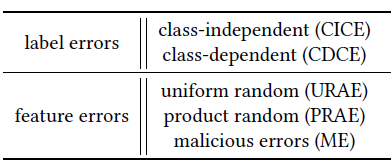
Table 1: Taxonomy of training data errors in the literature.
In this subsection, we review the literature on learning in the presence of training data errors most closely related to our work, where a more complete survey of the entire literature can be found. The error models can be categorized as either label errors or feature errors in Table 1, according to their classical definitions. Under each error model, the performance of a learning algorithm is analyzed against whether it achieves a desired classifier.
SETUP FOR RESILIENT BINARY CLASSIFICATION
THis section introduces essential definitions that are the bases for describing resilient binary classification problem. In the following subsections, we present a traditional binary linear classification problem, define our attacker assumptions, and introduce a resilience metric. Notationally, we write R, R+0 , N0 and [a;b] to denote the set of real numbers, non-negative real numbers, non-negative integers, and integers from a to b, respectively.
PROBLEM FORMULATION
This section formulates the problem of analyzing (and ultimately designing) resilient binary classification algorithms with respect to training data attacks. Specifically, given the number of positive and negative training data N, a set of classifiers F, a set of loss functions S, and a class of algorithms PF ;S, the goal of this paper is finding a classification algorithm P and a resilience bound g that minimize the error of the resilience bound such that P is g(N ; α)- resilient to a BFA. Here, to measure the error of the resilience bound.
RESILIENCE OF TRADITIONAL LINEAR CLASSIFICATION
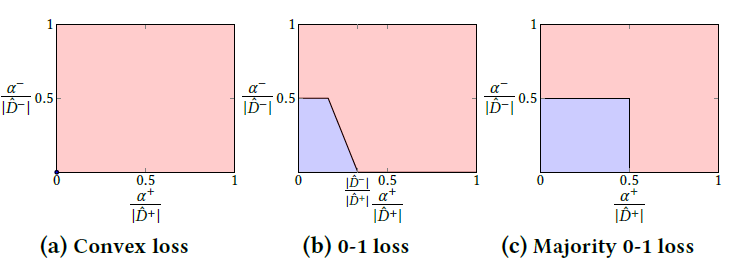
Figure 1: Perfectly attackable conditions on for each linear classification algorithm (colored in red).
This implies even though an attacker has weak ability to tamper training data, it can make the algorithm mis-classify all positive or all negative feature vectors of un-attacked training data by tampering only one positive or negative feature vector (See Figure 1a for the visualization of the perfectly attackable condition on α).
This proposition implies the 0-1 loss linear classification is strictly more resilient than convex one (See Figure 1b for comparison). Thus, different to the convex case, tampering single feature vector is not critical for the 0-1 loss linear classification. This means any CPS using convex linear classification algorithms can be converted into the 0-1 linear classification algorithm to defend against the single feature vector tampering.
RESILIENT LINEAR CLASSIFICATION
In this section, we propose a maximally resilient linear classification algorithm. A majority 0-1 loss linear classification is defined as PM; ℓ01 ∈ PL;S, where M denotes a majority constraint that restricts a feasible set of classifiers by only allowing a classifier that correctly classifies at least half of positive and negative feature vectors, according to
![]()
In the following subsections, the resilience proof and the worst-case resilience bound of the majority 0-1 classification are provided.
CASE STUDY
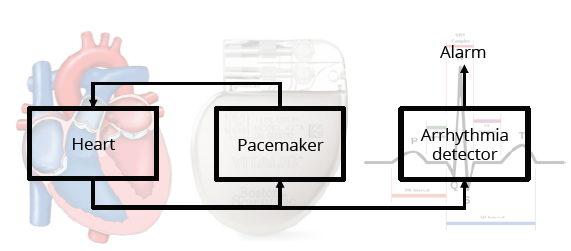
Figure 2: Pacemaker with an Arrhythmia detector.
We evaluated the resilience of traditional linear classification algorithms and the proposed algorithm using arrhythmia dataset. the arrhythmia, a.k.a irregular heartbeat, is a condition of the heart in which the heartbeat is irregular. An arrhythmia detector cooperated with logs from pacemaker can reduce stroke and death rate. To design such a detector, electrocardiogram (ECG) training data can be collected from logs of the pacemaker (Figure 2) whether ECG data is normal or abnormal (e.g., atrial fibrillation or sinus tachycardia).

Figure 3: The resilience of each linear classification algorithm under the specified attacks. The blue or red mark represents a positive or negative feature vector, respectively. The feature vector in the blue or red region is classified as positive or negative, respectively.
In Figure 3, the classification results of each linear classification algorithm, such as SVMs, the 0-1 loss linear classification, and the majority 0-1 loss linear classification, are illustrated with different types of an attack. The original training data without attacks is randomly drawn from two Gaussian distributions.
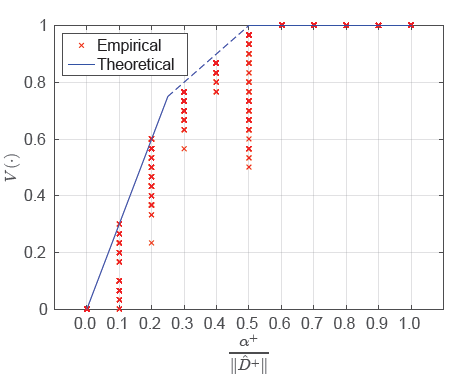
Figure 4: The degree of the resilience.
Figure 4: The degree of the resilience of PM; ℓ01 in the resilience metric V (.) with respect to the ability of an attacker. The blue solid and dashed line represents the theoretical robustness bound and the red cross means the empirically evaluated feasible resilience.
CONCLUSIONS
In particularly, the incorrect decisions on CPS directly affect on a physical environment, so learning techniques under training data attacks should be scrutinized. Toward the goal of resilient machine learning, we propose a resilience metric for the analysis and design of a resilient classification algorithm under training data attacks.
Traditional algorithms, such as convex loss linear classification algorithms and the 0-1 loss linear classification algorithm, are proved to be resilient under restricted conditions. However, the proposed 0-1 loss linear classification with a majority constraint is more resilient than others, and it is the maximally resilient algorithm among linear classification algorithms. The worst-case resilience bound of the proposed algorithm is then provided, suggesting how resilient the algorithm is under training data attacks.
Countermeasures. The resilience analysis on different linear classification algorithms provides us clues for countermeasures on training data attacks. Here, we briefly discuss a possible direction for countermeasures and its challenges. In general, additional algorithms can be considered to eliminate the worst-case situations in the analysis of each classification algorithm.
For example, to defend against the point attack on SVMs, it might be considered to add a pre-processing step that saturates large values in training data. Specifically, if a designer knows the minimum and maximum range of features, then range can saturate the large values that contribute to the point attack. However, this might not be an effective countermeasure since the range of features is not known in general and the point attack can be conducted after the pre-processing step, not before it.
Source: University of Pennsylvania
Authors: Sangdon Park | James Weimer | Insup Lee