ABSTRACT
Based on the monolayer growth mode of graphene sheets (2D crystal) by chemical vapor deposition (CVD) on a Cu surface, it should be possible to grow the 2D crystal embedded with single wall carbon nanocones (SWCNC) if nano-conical pits are pre-fabricated on the surface. However, a previous experiment showed that the growing graphene sheet can cross grain boundaries without bending, which seems to invalidate this route for growing SWCNCs.
The criterion of Gibbs free energy was applied in the present work to address this issue, showing that the sheet can grow into the valley of a boundary if the boundary has a slope instead of a quarter-turn shape, and SWCNCs can be obtained by this route as long as the lower diameter of the pre-fabricated pit is larger than 1.6 nm and the deposition temperature is higher than 750 K.
GROWTH ON THE CU GRAIN BOUNDARIES
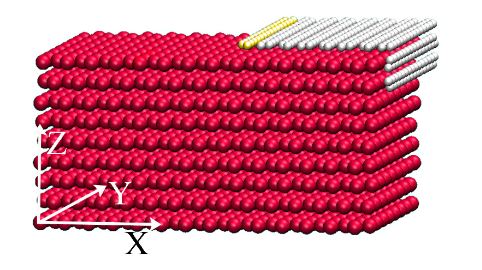
Figure 1: Schematic of a grain boundary with a quarter-turn shape covered by a piece of graphene sheet containing 290 C atoms
Regarding atomistic sizes, most crystal grain boundaries on metal surfaces should be of a quarter-turn shape, as shown in Figure 1. Therefore, we performed MD simulations on the relaxation of a piece of graphene sheet initially stuck to a quarter-turn boundary. Specifically, a Cu substrate of nine atomic layers with (111) surfaces was constructed according to the lattice constant 3.615°A, and the motion of a graphene sheet containing 290 carbon atoms placed on the quarter-turn boundary was simulated by MD.
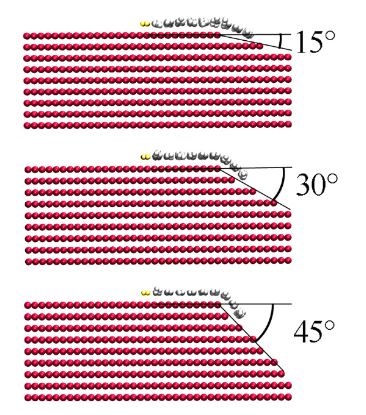
Figure 2. The structure of a piece of graphene sheet consisting of 290 C atoms on different slopes of the grain boundary after 200 ps relaxation at 1200 K
For example, when the mobile C atoms were initially assigned velocities of Maxwell distribution at 300 K, the bent sheet also turned into a flat structure in about 50 ps. However, things changed when the quarter-turn boundary was replaced with a slope of bent angles of 15◦, 30◦, and 45◦, as shown in Figure 2. After the mobile C atoms were assigned the velocities of Maxwell distribution at 1200 K, the graphene sheet kept the curved shape until the end of the MD simulation, at 200 ps.
SWCNC GROWTH BY CVD METHODS
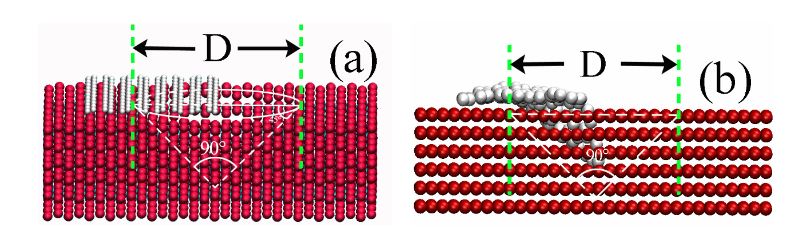
Figure 4. (a) Schematic of a piece of flat graphene sheet covering half of a conical pit with an angle of 90◦; or (b) the sheet bending into the pit
However, the realistic growth rate of graphene by CVD is too slow for MD to simulate, and we have to resort to the GFE criterion that states for an isobaric process, such as CVD growth, the system tends to a structure of lower GFE. Therefore, we calculated the GFE of a piece of graphene sheet crossing over a pit on the surface (Figure 4a), or bending into the pit (Figure 4b), to see which geometry is of smaller GFE.
CONCLUSIONS
Based on the GFE criterion, it is shown that single wall carbon nanocones embedded in single layer graphene sheets can be obtained by CVD on a Cu surface with pre-existing conical pits. For a 90◦ conical angle, the growth requires that the lower diameter of the pit must be larger than 1.6 nm and the temperature of the substrate should be higher than 750 K, which is below the temperature required for the CVD growth of graphene.
Certainly, it is necessary to understand the dynamics of how the carbon atoms move into the pit to form the nanocone, but the process is too slow to be simulated by MD, so the specific pathway or mechanism for the nanocone growth and the exact structures of the bent sheet still escape prediction.
Source: Fudan University
Authors: Yu-Peng Liu | Jing-Tian Li | Quan Song | Jun Zhuang | Xi-Jing Ning