ABSTRACT
Since Findler and Felleisen (Findler, R. B. & Felleisen, M. 2002) introduced higher-order contracts, many variants have been proposed. Broadly, these fall into two groups: some follow Findler and Felleisen (2002) in using latent contracts, purely dynamic checks that are transparent to the type system; others use manifest contracts, where refinement types record the most recent check that has been applied to each value.
These two approaches are commonly assumed to be equivalent—different ways of implementing the same idea, one retaining a simple type system, and the other providing more static information. Our goal is to formalize and clarify this folklore understanding. Our work extends that of Gronski and Flanagan (Gronski, J. & Flanagan, C. 2007), who defined a latent calculus λC and a manifest calculus λH, gave a translation φ from λC to λH, and proved that if a λC term reduces to a constant, so does its φ-image.
We enrich their account with a translation ψ from λH to λC and prove an analogous theorem. We then generalize the whole framework to dependent contracts, whose predicates can mention free variables. This extension is both pragmatically crucial, supporting a much more interesting range of contracts, and theoretically challenging. We define dependent versions of λH and two dialects (“lax” and “picky”) of λC, establish type soundness—a substantial result in itself, for λH – and extend φ and ψ accordingly. Surprisingly, the intuition that the latent and manifest systems are equivalent now breaks down: the extended translations preserve behavior in one direction, but in the other, sometimes yield terms that blame more.
THE NON-DEPENDENT LANGUAGES
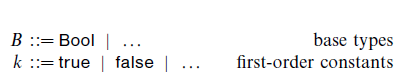
Fig. 2. Base types and constants for λC and λH.
We begin in this section by defining the non-dependent versions of λCand λH and continue with the translations between them. The dependent languages, dependent translations, and their properties are developed. Throughout the paper, rules prefixed with an E or an F are operational rules for λC and λH, respectively. An initial T is used for λC typing rules; typing rules beginning with an S belong to λH. All of our languages will share a set of base types and first-order constants, given in Figure 2. Let the set KB contain constants of base type B. We assume that Bool is among the base types, with KBool = {true, false}.
The operational semantics is given in Figure 3. It includes six rules for basic (small-step, CBV) reductions, plus two rules that involve evaluation contexts E (Figure 3). The evaluation contexts implement left-to-right evaluation for function application. If ⇑ l appears in the active position of an evaluation context, it is propagated to the top level, like an uncatchable exception. As usual, values (and results) do not step.
THE NON-DEPENDENT TRANSLATIONS
The latent and manifest calculi differ in a few respects. Obviously, λC uses contract application and λH uses casts. Second, λC contracts have two labels—positive and negative—where λH contracts have a single label. Finally, λH has a much richer type system than λC. Our ψ from λH to λC and Gronski and Flanagan’s φ (2007) from λC to λH must account for these differences while carefully mapping “feature for feature.”
The interesting parts of the translations deal with contracts and casts. Everything else is translated homomorphically, though the type annotation on lambdas must be chosen carefully. The full definitions of these translations the non-dependent definitions are a straightforward restriction.
THE DEPENDENT LANGUAGES
Now we come to the challenging part: Dependent λH and its proof of type soundness. These results require the most complex metatheory in the paper because we need some strong properties about CBV evaluation.3 The full definitions are in Figures 6 and 7. As before, we have marked the changed rules with a • next to their names.
We can show that the two type semantics are in fact equal using a parallel reduction technique. We define a parallel reduction relation ⇒ on terms and types in Figure 9 that allows redexes in different parts of a term (or type) to be reduced in the same step, and we prove that types that parallel-reduce to each other—like S2 {x := s2} and S2 {x := q2}—have the same semantics.
THE TRANSLATIONS
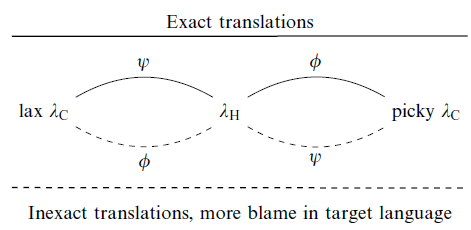
We divide our treatment of translations between lax λc, λH, and picky λc into two sections: one for exact translations, moving right on the axis of blame, and another for inexact translations, moving left.
Each translation proof follows the same basic schema. First, we define a logical relation between the two languages. Then we use the logical relation to prove a lemma relating the translation, contracts, and casts.
EXACT TRANSLATIONS

Fig. 10. A blame-exact result/term correspondence.
Translations moving left on the axis of blame—from picky λc to λH, and from λH to lax λc—are exact. That is, we can show a tight behavioral correspondence between terms and their translations (see Figure 10). We read t ∼ s : T as “t corresponds with s at type T.” Our correspondence is a standard logical relation, defined in two intertwined parts: a relation on results, r ≈ q : T and its closure with respect to evaluation, t ∼ s : T.

Fig. 14. Blame-exact correspondence for ψ into lax λC.
We reuse the term correspondence t ∼ s : T (Figure 10), interpreting it as using −→lax, and define a new contract/cast correspondence c ∼ S1 ⇒l S2 : T (Figure 14), relating contracts and pairs of λH types—effectively, casts. This correspondence uses the term correspondence in the base type case and follows the pattern of F_CDECOMP in the function case.
Since it inserts a cast in the function case, we index the relation with a label, just like ψ. Note that the correspondence is blame-exact, relating λC and λH terms that either blame the same label or go to corresponding values. We define closing substitutions ignoring the contracts in the context; we lift the relation to open terms in the standard way.
INEXACT TRANSLATIONS

Fig. 15. Blame-inexact correspondence for φ from lax λC.
We can show the behavioral correspondence using a blame-inexact logical relation, defined in Figure 15. The behavioral correspondence here, though weaker than before, is still pretty strong: if t ∼> s : B (read “t blames no more than s at type B”), then either s −→∗h ⇑l or t and s both go to k ∈KB . This correspondence differs slightly in construction from the earlier exact one—we define ≈> as a relation on values, while ≈ is a relation on results.
RELATED WORK
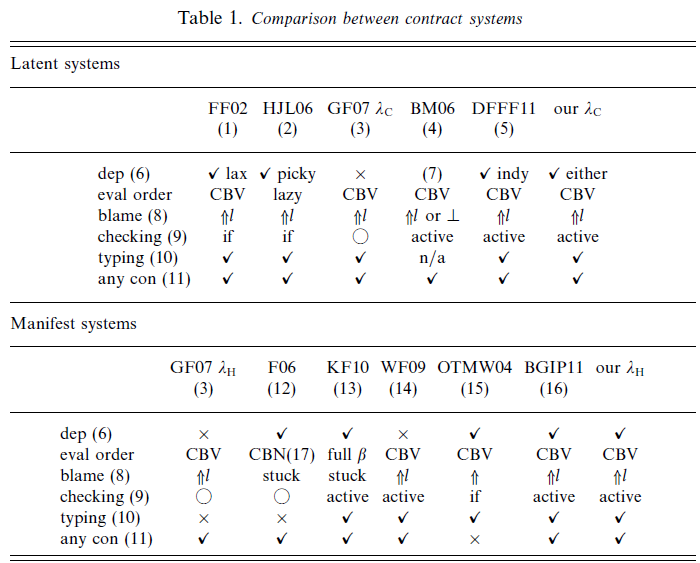
Conferences in recent years have seen a profusion of papers on higher-order contracts and related features. This is all to the good, but for newcomers to the area it can be a bit overwhelming, especially given the great variety of technical approaches. To help reduce the level of confusion, in Table 1 we summarize the important points of comparison between a number of systems that are closely related to ours. This table is an updated version compared to that in Greenberg et al.
CONCLUSION
We can faithfully encode dependent λH into λC—the behavioral correspondence is tight. λH’s F_CDECOMP rule forces us to accept a weaker behavioral correspondence when encoding λC into λH, so we conclude that the manifest and latent approaches are not equivalent in the dependent case. We do find, however, that the two approaches are entirely inter-encodable in the non-dependent restriction.
Source: University of Pennsylvania
Authors: Michael Greenberg | Benjamin C. Pierce | Stephanie Weirich


