ABSTRACT
Transport-category or FAR/CS 25 certified airplanes may occasionally become braking energy capacity limited. Such limitation may exist when heavy airplanes are departing airports at high-density altitudes, on relatively long runways, and/or possibly with some tailwind component. A maximum braking energy VMBE speed exists which may limit the maximum allowable takeoff decision/action speed V1. The ever-existing possibility of high-speed rejected takeoff in such conditions may also limit the airplane gross weight for declared available distances.
To gain deeper insights and acquire better understanding of the topic, a theoretical model of the maximum braking energy and the related VMBE speed for T-category airplanes was developed. The total kinetic energy of an airplane includes translational and rotary kinetic energy and the potential height-energy component for sloped runways. Time-dependent airplanes’ mechanical power expression has been derived. Weight transfer during dynamic braking has been implemented in the full nonlinear model.
Added mass due to rotary inertia of spinning components has been incorporated and assumed constant. The brakes thermal model is based on a lumpedparameter analysis of ventilated brake rotors and stators; the thermal model is based on a small Biot-number approximation and sufficiently well describes the physics of friction braking. The nonlinear differential equations of motion and the differential thermal model are coupled. A nonlinear model incorporating a set of ordinary differential equations with tire slip can be solved numerically.
This model enables determination of the entire history of translational and angular accelerations and speeds, longitudinal distance, forces, torque, and disc temperature during braking. A simpler model assuming constant physical and thermodynamic parameters is solved analytically for constant negative acceleration. This linear analytical model has been used as a workhorse method in our calculations. A new semiempirical expression of temperature-dependent friction coefficient on brake rotor-stator pairs has been proposed.
A theoretical model of maximum braking energy speed VMBE, which includes density-altitude, runway slope, and wind effects as parameters, has been developed for the first time to the best of our knowledge. A comparison of the theoretical VMBE model showed good agreement with measured and approved data for the B737-400 airplane at different density altitudes with and without, individual and combined, runway slope and tailwind effects. Results for new and fully worn brakes were obtained showing the effect of elevated temperatures on brake fade and consequently braking time and distance.
LITERATURE REVIEW
It is somewhat surprising that little to no research is being published on airplane braking systems, dynamics/physics, and operational limitations. To the best knowledge of this author, no publically available archived material exists on the direct problem of VMBE determination and the related theoretical braking energy considerations.
Engineering and pilot-oriented books and publications provide very little insight into MBE and related issues. That is no surprise, as one has to simultaneously tackle problems of ground-effect aerodynamics, thermodynamics, heat transfer, and tribology. Ample published material on design of automotive braking systems exists, which was somewhat useful.
METHODS AND MATERIALS
The old FAR 25.735 (Amendment 25-92 from 1998) introduced various new design criteria for T-category airplane brakes approval. Different sections of FAR 25 address landing and RTO kinetic energy capacity and requirements for brakes. Essentially, qualification testing using fully worn brakes of its allowable wear range is required.
The brake kinetic energy requirement must be based on a rational analysis of the sequence of events expected during RTO. Alternatively, the old FAR 25.735(h)(2) allows the kinetic braking energy requirement for each braked main wheel to be derived using the following relationship (FAA, 2000):
KE = 0:0443 x W x v2 / N
Here, KE is kinetic energy per braked wheel in ft-lbf, N is the number of braked main wheels, W is airplane weight in lbf at which kinetic energy absorption is being evaluated, and V is speed in knots.
MATHEMATICAL MODEL OF FRICTION BRAKING
A mathematical model of braking action of FAR/CS 25 certified T-category airplanes is now presented. A rigid airplane braking model including the rotary inertia of wheels, discs, tires, and axles is developed. The runway is assumed smooth with a small positive or negative average incline to simulate uphill or downhill takeoffs and landings. Newtonian laws of classical mechanics in a topo centric, non-rotating, flat earth quasi-inertial frame-of-reference are assumed for short braking action durations and distances.
WEIGHT TRANSFER DURING DYNAMIC BRAKING
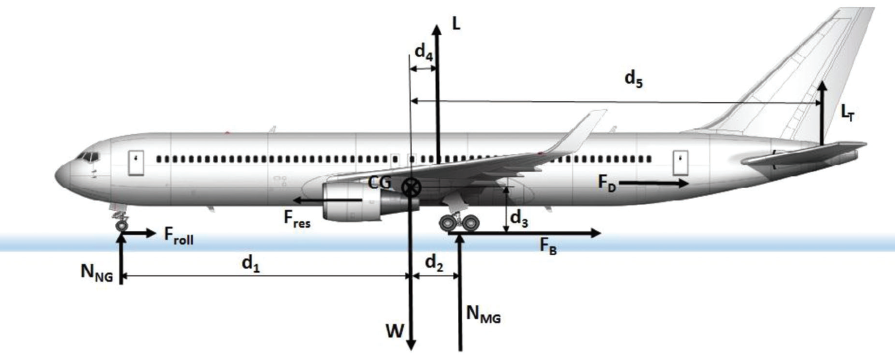
Figure 2. Forces and torques on NG and MG during static and dynamic-braking conditions.
When the airplane is static on the ground most of the weight is supported by MGs. The CG of an airplane is between the NG and MGs, but quite closer to MGs. Using the illustration from Figure 2, the location of the CG, and the static force and momentum balance, the normal reaction on the NG and MGs can be calculated from:
NNG ⋅ d1 – NMG ⋅ d2 = 0 NNG + NMG = W
d1+d2 = wb = const
Here, wb designates a wheelbase (WB), which is constant for a specific airplane model (see also Daidzic, 2016c). CG can move between the maximum forward and aft limits.
ENERGY CONSIDERATIONS DURING BRAKING
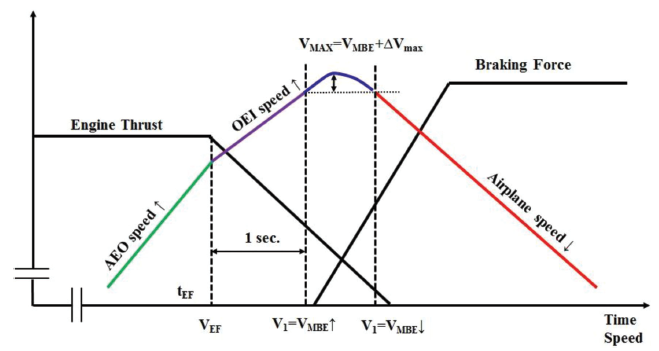
Figure 3. Engine failure and acceleration transition region. Not to scale.
The total energy and the instantaneous power will be maximum at the braking onset and will decrease to zero over length and time. As the first action is taken to stop an airplane and the brakes are first applied (FAR 25.109), the aircraft will still have some residual acceleration and the maximum speed reached before deceleration is a bit higher than VMBE as illustrated in Figure 3.
THERMAL ENERGY CONSIDERATIONS DURING FRICTIONAL BRAKING
Due to intense heating, brakes must be cooled (convective and radiative). However, for the short duration of maximum effort braking, we can assume that the entire mechanical energy is being absorbed by break discs. Thermodynamic equilibrium considerations lead to a simple relationship for temperature rise in brake discs, ΔTB=EMBE / MB ⋅ cB. To illustrate this, let us take an airplane that weighs 410,000 lbf (mass is 186,364 kg) taking off on a level dry runway and no wind. The airplane has eight wheels/tires in dual-axle configuration (four wheels per main landing gear bogie).
BRAKE FRICTION MATERIALS AND FLUIDS
Some basic brake disc/rotor physical and thermal material properties, mostly at 20oC and for aerospace use, are presented in Table 1 (Breuer & Bill, 2008; Daidzic, 2016c; Holman, 1986; Ozisik, 1985). Specific heat capacity, thermal conductivity, and temperature limits are preferred high, while thermal expansion is desirably low. Large variations in thermal properties exist depending on the exact composition of materials used. For example, Silicon- Carbide (SiC) can have a specific heat capacity of 1,420 J/kg K at low temperatures.
B737 BRAKES AND LANDING GEAR
Boeing 737-400 (classic series) is a 150,000 lbf (68 metric ton) MSTOW airplane. According to Brady (2016), the classic series B737 (300/400/500) brakes are made of steel-alloy (metal-ceramic) with the trade name Cerametalix®, and with versions made by either Goodrich or Honeywell. Since 2008, the carbon-brake option has been available for the B737NG (Allen et al., 2009) from either UTCAerospace systems (formerly Goodrich) with DURACARB® carbon technology, or Safran© (formerly Messier-Bugatti) with SepCarb III OR (Oxidant Resistant) technology.
RESULTS AND DISCUSSION
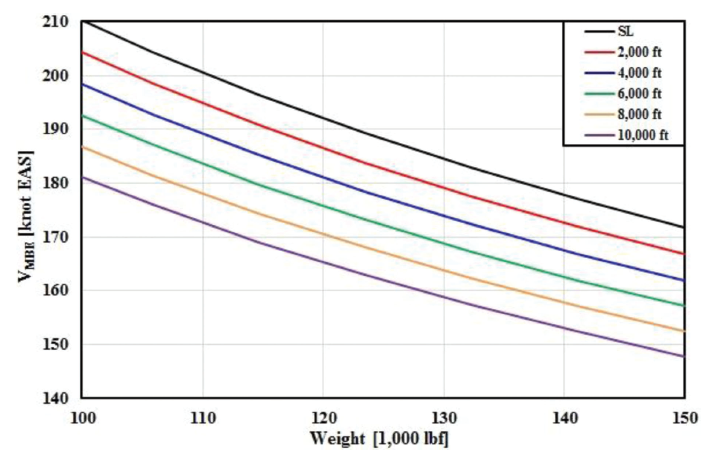
.Figure 4. Computational results of VMBE for B737-400 with steel-alloy brakes at various pressure altitudes with standard temperatures, level runway, and no wind.
Computations of the VMBE for B737-400 airplanes equipped with steel-brakes as a function of TOW, and various DAs as parameters for dry & level runway and no wind, are shown in Figure 4. Equation (18) was used to estimate MBE speed (EAS/CAS). Standard temperatures and barometer setting are used so that MSL elevation (local Geoid height), PA (pressure altitude), and DA are all equal.
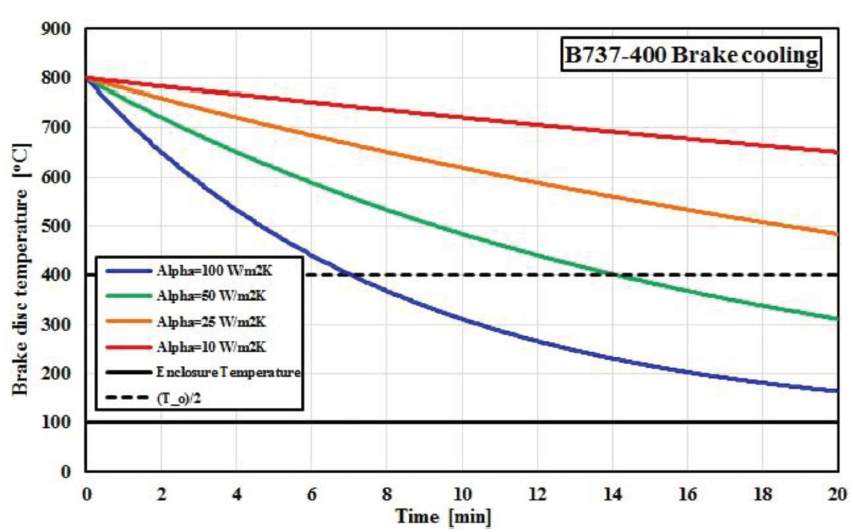
Figure 9. Brake cooling for steel-alloy B737-400 brake model as a function of time and different cooling efficiencies.
To estimate the time required for brake cooling after application, we used a theory presented in Appendix C. Computational results for different cooling efficiencies are summarized in Figure 9. One of the cooling scenarios uses B737-400 steel-alloy brakes, but now with the average combined heat transfer coefficient of 50 W/m2K (D = 0.001), to simulate reduced efficiency of ventilated rotors due to dirt accumulation and corrosion.
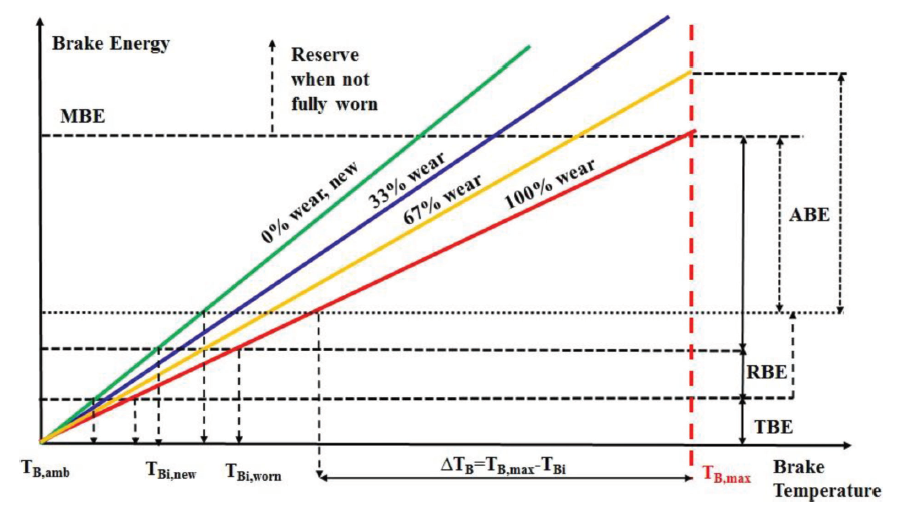
Figure 10. Braking energy considerations regarding brake heat-pack temperature for various brake wear states. Not to scale.
Taxiing necessitates use of brakes, and taxiing brake energy (TBE) further reduces ABE. For example, A320 increases thermal load on the brakes by about 5 MJ during standard taxiing. The relationship between the MBE, ABE, RBE, and TBE as a function of brake temperature and brake wear is illustrated in Figure 10.
CONCLUSIONS
In this article, the theoretical model of the maximum braking energy and the related VMBE speed for T-category airplanes was developed. The total kinetic energy of an airplane includes translational and rotary kinetic energy and the potential height-energy component for sloped runways. Time-dependent airplanes’ mechanical power expression has been derived. The brake thermal model is based on a lumped-parameter analysis of ventilated brake heat packs. The thermal model is based on the small Biot-number lumped-parameter approximation and sufficiently describes the basic physics of the friction braking.
The nonlinear differential equations of motion and the differential thermal model are coupled. A nonlinear set of ordinary differential equations incorporating tire slip can be solved numerically. A simple linear airplane braking model using average parameters and coefficients was developed for the first time to the best of our knowledge. The analytical solution for the constant deceleration thermal problem was derived. Additionally, the semi-empirical expression of temperature dependent COF on a rotor-stator pair has been proposed.
The presented mathematical model enables determination of the entire history of translational and angular accelerations and speeds, longitudinal distance, forces, torques, and disc temperatures during braking. Weight transfer during dynamic braking has been implemented in brake force determination. Added mass due to rotary inertia of spinning components has been incorporated and assumed constant for simplicity. Added mass for rotary inertia is indeed very small for airplanes. A theoretical model of VMBE which includes density altitude, runway slope, and wind effects as parameters has been developed for the first time to the best of our knowledge. A comparison of the theoretical VMBE model showed good agreement with the measured and approved AFM data for the B737-400 airplane at different DAs with and without, individual and combined, runway slope and tailwind effects.
Source: JATE
Authors: Nihad E. Daidzic
>> 200+ IoT Led Projects for Final Year Students