ABSTRACT
Self-consistent field theory (SCFT) has proven to be a powerful tool for modeling equilibrium microstructures of soft materials, particularly for multiblock polymers. A very successful approach to numerically solving the SCFT set of equations is based on using a spectral approach. While widely successful, this approach has limitations especially in the context of current technologically relevant applications.
These limitations include non-trivial approaches for modeling complex geometries, difficulties in extending to non- periodic domains, as well as non-trivial extensions for spatial adaptivity. As a viable alternative to spectral schemes, we develop a finite element formulation of the SCFT paradigm for calculating equilibrium polymer morphologies. We discuss the formulation and address implementation challenges that ensure accuracy and efficiency.
We explore higher order chain contour steppers that are efficiently implemented with Richardson Extrapolation. This approach is highly scalable and suitable for systems with arbitrary shapes. We show spatial and temporal convergence and illustrate scaling on up to 2048 cores. Finally, we illustrate confinement effects for selected complex geometries. This has implications for materials design for nanoscale applications where dimensions are such that equilibrium morphologies dramatically differ from the bulk phases.
SELF CONSISTENT FIELD THEORY EQUATIONS
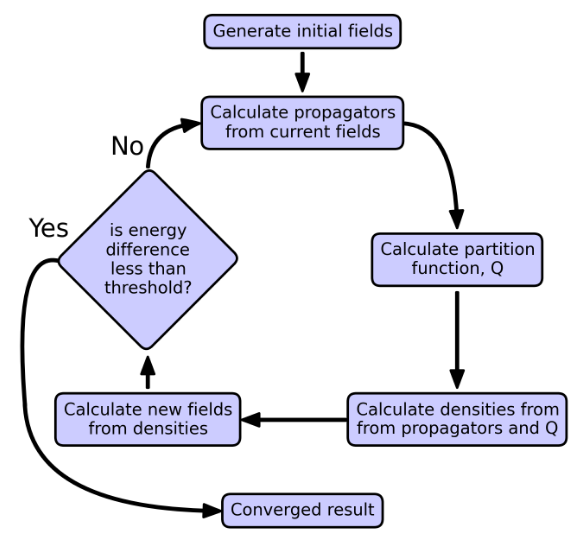
Figure 2: Flowchart of SCFT iterative process.
Finding the mean field state is done through an iterative process. The overall sequence of the solution, as illustrated in figure 2, consists of five main steps: initial field generation, propagator calculation, partition function calculation, density calculation, and field recalculation. This approach is equivalent to solving a fixed point problem for the field: W = F(W).
PROPAGATOR FORMULATION
Since the propagator is the most computationally demanding part of the solution process, we discuss the implementation in detail. This section presents the solution of the propagator using finite elements. It gives the weak form and matrix form of the propagator equation. Following that, several methods of discretizing the contour derivative are presented using a typical contour stepping solving scheme.
- Variational Form
- Semi-discrete Matrix Form
- Discrete Form
FINITE ELEMENT IMPLEMENTATION

Figure 3: Gyroid phase of diblock polymer.
As a basis for comparison, we use a cubic system with an edge length of 8.82 times the polymer radius of gyration (Rg). The diblock chain is 40% A and 60% B (which corresponds to an A block fraction, f, of 0.4) with an interaction parameter of χN = 14.4. This corresponds to a 3D gyroid phase of the diblock polymer (see figure 3). In this case, bA = bB, making the A and B blocks indistinguishable. The spectrally determined Q value is 5.32583.
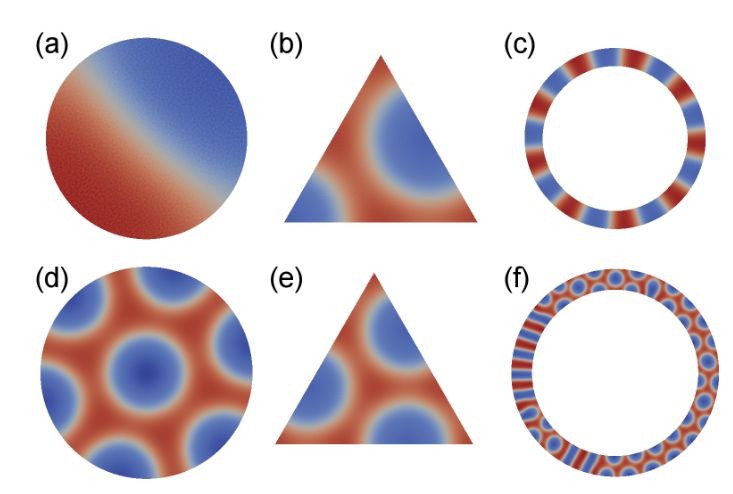
Figure 6: 2D structures using a non-uniform, non-square mesh.
Figure 6: 2D structures using a non-uniform, non-square mesh. For all cases χN = 14.4, f = 0.4, and zero-flux boundary conditions were applied. The circle in (a) has a radius of 1 Rg, while (d) has a radius of 4 Rg. The triangle in (b) has an edge length of 4 Rg, while (e) has an edge length of 6 Rg. The annulus in (c) has an outer radius of 5 Rg and an inner radius of 4 Rg, while (f) has an outer radius of 18 Rg and an inner radius of 14.4 Rg.
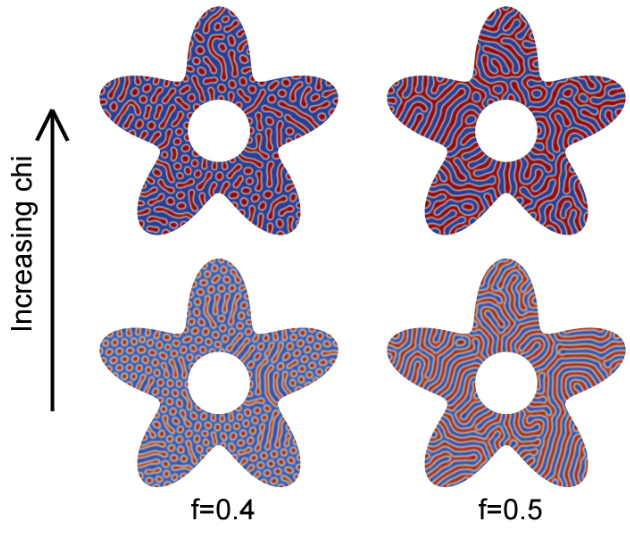
Figure 8: 2D structures using a non-uniform mesh to show variation.
Figure 8: 2D structures using a non-uniform mesh to show variation with fraction of A chain (f) and χN values. The top row of images has χN = 25 while the bottom row has χN = 14.4. In all cases, the distance from the center to the outer most point is 10 Rg and zero-flux boundary conditions were used.
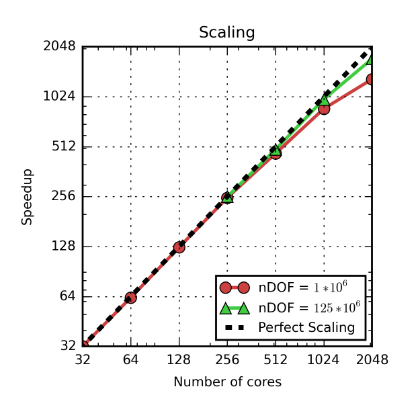
Figure 10: Strong scaling results using quadratic basis functions on the blue waters system. nDOF = number of degrees of freedom being solved in the system. Dashed black line shows perfect linear scaling.
Another key advantage of the finite element approach is the ability to run very large problems on multiple processors with high efficiency. For most periodic systems or unit cell calculations, this is not an important consideration. However, for complex geometries or more complicated chain models, efficient scaling allows modeling large systems. The benefit comes from the near linear scaling of the finite element approach. This allows running problems on a wide range of system sizes. Figure 10 shows scaling results up to 2048 cores using this model on a diblock polymer system. These results were generated on the Blue Waters system
CONCLUSION
The finite element method discussed in this paper is an alternative to the standard spectral and pseudo-spectral methods for self-consistent field theory calculations. The use of this alternate approach has advantages when considering large problems with non- periodic geometries. We have discussed details of the implementation relevant to the accurate simulation of block copolymer systems. Use of a finite element method for SCFT allows easy calculation of self-assembled structures in complex geometries.
This has implications for the study of thin film and other confined systems beyond a simple bulk melt. The scalability of the approach allows larger structures to be calculated, enabling simulation of physically relevant sizes. While our focus is on the common diblock case, the method can be applied to multiblock polymers with an arbitrary number of blocks and non-linear architectures. Beyond the benefits shown here, the SCFT approach also has potential application to chain models other than the Gaussian chain, which are becoming of more interest as the power of computational resources expand.
Source: Iowa State University
Authors: David M. Ackerman | Kris Delaney | Glenn H. Fredrickson | Baskar Ganapathysubramanian