ABSTRACT:
Closed, steady or cyclic thermodynamic systems, which have temperature variations over their boundaries, can represent an extremely large range of plants, devices or natural objects, such as combined heating, cooling and power plants, computers and data centres, and planets.
Energy transfer rates can occur across the boundary, which are characterized as heat or work. We focus on the finite time thermodynamics aspects, on energy-based performance parameters, on rational efficiency and on the environmental reference temperature.
To do this, we examine the net work rate of a closed, steady or cyclic system bounded by thermal resistances linked to isothermal reservoirs in terms of the first and second laws of thermodynamics. Citing relevant references from the literature, we propose a methodology that can improve the thermodynamic analysis of an energy-transforming or an exergy-destroying plant.
Through the reflections and analysis presented, we have found an explanation of the second law that clarifies the link between the Clausius integral of heat over temperature and the reference temperature of the Gouy–Stodola theorem. With this insight and approach, the specification of the environmental reference temperature in exergy analysis becomes more solid.
We have explained the relationship between the Curzon Ahlborn heat engine and an irreversible Carnot heat engine. We have outlined the nature of subsystem rational efficiencies and have found Rant’s anergy to play an important role. We postulate that heat transfer through thermal resistance is the sole basis of irreversibility.
SNIPPETS:
Model:
As an actual ‘environment’ may not be in thermal equilibrium: a real plant may interact with multiple thermal reservoirs, e.g., with the ground, with a large body of water, with the air, with the sun and with the sky, as well as available sources of exergy, such as a combustion region or a source of waste heat.
Usually, also, there will be at least one intended exergy sink, which needs to be adequately defined and characterized: it could be a sink of mechanical shaft power, a sink of electrical power or, as a pertinent example, an isothermal reservoir attached to the system by a thermal resistance.
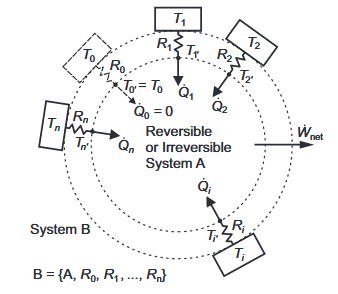
A Closed Reversible or Irreversible System, A, Bounded by Constant Thermal Resistances Linked to Isothermal Reservoirs.
As a key constraint, we assume that System A undergoes no net change. For simplicity, we assume that it is closed, as otherwise we would have of include net transport of energy and entropy in our energy and entropy balances. It may be in a steady state, but if its state is unsteady, the net work interaction rate is the time-averaged value, and the heat transfer rates are time-averaged values at stated fixed temperatures.
CONCEPT DEVELOPMENT
We adopt a methodology that may help us to extract the structure of and appreciate the nature of the exergy flow paths associated with heat transfer, provide insight into ways of defining rational efficiency in exergy analysis and make the choice of environmental reference temperature somewhat more solid and method based, recognizing the significance of finite time in real thermodynamic processes that involve heat transfer. We start with the simplest case and develop the concepts progressively.
One Heat Source and One Heat Sink With Reversible Heat Transfer:
In Figure 2, a system, A, has a net work interaction while exchanging heat with just two isothermal reservoirs, at temperatures T1 and T0, where each thermal reservoir is linked to the boundary of the system, without any thermal resistance between them. For the moment, we assume the net work is an energy output and that T1> T0. We also assume that System A undergoes only reversible processes.
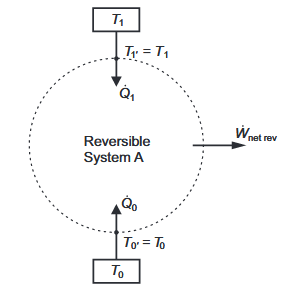
Figure 2. A Closed Reversible System, a, Bounded By Two Isothermal Reservoirs, Without Intermediate Thermal Resistances.
One Heat Source and One Heat Sink with Thermal Resistances:
Assuming an HE1 heat engine (T1> T0), taking into account the temperature drops associated with heat transfer through resistances R1 and R0 in Figure 3 and letting Rtot = R1+R0, the thermal efficiency is given by Equation (11) and the net power output by Equation (12).
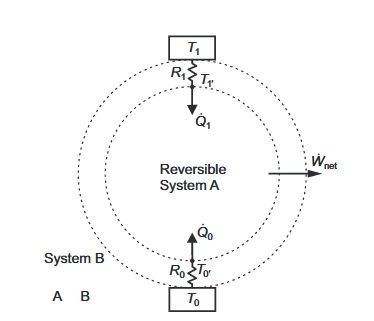
Figure 3. A Closed Reversible System, A, Bounded By Two Constant Thermal Resistances Linked to Isothermal Reservoirs.
Heat Input Rate and Thermal Efficiency of a Heat Engine at Maximum Power:
For an HE1 heat engine (where T1> T0) at maximum net power output, the rate of heat input is given by Equation (19) and the thermal efficiency by Equation (20).
Exergy Analysis Principles to Be Applied:
The equality of Clausius, Equation (25), applies to the reversible system, A, of Figure 3, while his inequality, Equation (26), applies to the irreversible system, B, that includes the thermal resistances.
Exergy Analysis of a Reversible System Linked without Thermal Resistances to Its Heat Source and Sink:
We now apply exergy analysis to the reversible heat engine, A, described in Section 2.1 and Figure 2.We take T0 to be the temperature of the environment. The net rate of work W net rev is equivalent to a rate of shaft work, so it is also a rate of exergy transfer. If T1=T0, W net rev can only be zero, and all rates of exergy output are zero, so the rational efficiency is undefined and irrelevant. In all other cases, the rational efficiency is unity.
Exergy Analysis of a Reversible System Linked to Its Heat Source and Sink by Thermal Resistances:
We now apply exergy analysis to Heat Engine B described in. If T1=T0, ̇W net can only be negative (i.e., an exergy input rate) or zero. The rates of exergy output can only be zero, so the rational efficiency is zero when W net is negative.
THE ENVIRONMENTAL TEMPERATURE AND MULTIPLE ISOTHERMAL RESERVOIRS
Exergy analysis is built on the assumption of an enclosing environment that has a temperature that is at least approximately constant, and much consideration has been given to the concept of the environmental dead state . Here, we use the configuration of Figure 1 to explore the meaning of T0.
One Heat Source and Two Environmental Heat Sinks:
We now consider System A, as in Figure 1, with one heat source at T1 and two environmental thermal reservoirs at temperatures T2 and T3. As a concrete real-world example, heat rejection could occur from a heat engine to ambient air at 25◦C and to seawater at 13◦C.
We use the term ‘environmental’ thermal reservoir to signify that any heat transfer with that reservoir has no intrinsic value, other than balancing the energy inputs and outputs of the steady or cyclic system in accordance with the first and second laws of thermodynamics.
Generalization for Multiple Thermal Reservoirs:
Now, we apply a technique like the one that Clausius used for cycles described on a thermodynamic state diagram, which we mentioned in Section 1.1. Rather than imagining thin Carnot cycle strips on a p–V diagram, we imagine thin 3D bi-thermal (interacting with two isothermal reservoirs) closed, steady or cyclic systems.
By aggregating them side-by-side, we can construct an arbitrary multi-thermal closed, steady or cyclic system. Each bi-thermal element of the side-by-side aggregation of subsystems has a hot surface, a cold surface and surfaces that are adiabatic. We can arrange them so that our composite system operates with a range of high and low temperatures distributed over the composite surface. The inequality of Clausius applies to our composite system where the integral is performed over the composite external surface and over time.
The Nature of the Environmental Reference Temperature:
We propose the following generalization of the definition of T0. Our first realization is that the generalized System B, surrounded by many thermal reservoirs, is characterized by two temperatures, TH avg and TL avg, the equivalent average high and low temperatures of the boundary at which the entropy acceptance and entropy rejection rates occur, as defined in Equations (60)–(65).
METHODOLOGY SUGGESTIONS
We have shown that for a closed, steady or cyclic system, the average rate of exergy destruction, also known as the lost work rate or the irreversibility rate, can be evaluated and the rational efficiency of the system calculated.
If we can partition the overall system into subsystems that are also closed and steady or cyclic, then we can evaluate the average rates of exergy destruction and the rational efficiencies of those subsystems, as well.
THE IRREVERSIBLE CARNOT SYSTEM OF FINITE THERMAL RESISTANCE
We denote any system of the type shown in Figure 2 as a reversible Carnot system, as it corresponds to the class of systems that Carnot described in 1824. This class could employ a vapour (two phase),gaseous, liquid or solid medium—Carnot indicated he did not favour liquid or solid.
He specified that only infinitesimal temperature differences for heat transfer should subsist in his ideal heat engine. Thus,the working medium would have only infinitesimal thermal resistance, or would require infinite time to produce a finite net work output. Carnot also clearly stated that all temperature changes within the working medium were to be due to compression and expansion only.
OVERALL AND SUBSYSTEM RATIONAL EFFICIENCIES
Whenever we evaluate a rational efficiency for an overall closed, steady or cyclic plant there is the presumption that, in principle, the plant could be replaced with a perfect thermodynamic device that would have a rational efficiency of unity when interacting with the same exergetic resource and the same environment. The rate of exergy supply from the exergetic resource is always positive. The exegetic resource may be a thermal reservoir with an ‘above ambient’effective temperature, or one with a ‘below ambient’ effective temperature.
CONCLUSIONS
The model of a closed reversible or irreversible system linked by constant resistances to isothermal reservoirs provides useful insights into finite time, or irreversible, thermodynamics. The temperature versus entropy transfer rate method can localize exergy destruction rates and provide subsystem rational efficiencies.
Without going to extraordinary lengths, a methodical approach can be used to specify an appropriate thermal reference environment model as part of an overall exergy analysis approach, respecting the principles of finite time thermodynamics. We have shown that the reference environment need not necessarily be at a single constant temperature.
By expressing the second law of thermodynamics in terms of the net exergy input rate to a closed, steady or cyclic system that undergoes no net change, we have clarified the link between the Clausius integral of heat over temperature and the reference temperature of the Gouy–Stodola theorem.
We have demonstrated the equivalence of the Curzon Ahlborn system and the irreversible Carnot system. We have also outlined how subsystem rational efficiencies relate to overall rational efficiency.
We have found that Rant’s anergy is in fact a very important concept for the analysis of heat and work rates over the boundary of a system. From the evidence we have presented, we postulate that heat transfer through thermal resistance is the sole basis of irreversibility.
Source: Dublin Institute of Technology
Author: Jim A. Mc Govern
