ABSTRACT
Planar bar-and-joint mechanisms with one degree-of-freedom are widely used in deployable structures and machines. Such mechanisms are designed to undergo a specific motion, which can be described mathematically by plotting out the compatibility conditions, resulting in a curve called compatibility path.
This dissertation studies singularities occurring in compatibility paths with the aid of knowledge in the theory of structural stability. It has been observed that compatibility paths can develop singularities similar to that of equilibrium paths of elastic structures.
An analogy is set up between the equilibrium path of elastic structures and the compatibility path of mechanisms with a single degree-of-freedom incorporating the different types of bifurcation, effects of imperfections and detection of singularities. It is shown that the fundamentally distinct critical points such as limit points and bifurcation points can also appear in compatibility path. Methods used to singularities for compatibility conditions of mechanisms and equilibrium of structures are unified so that they can be used for both cases. A formulation of potential energy for mechanisms is also proposed in analogy with the potential energy function used in structural analysis.
Further analysis of the mechanisms is carried out to demonstrate that singularities of compatibility paths can also be dealt with by the elementary catastrophe theory similar to the stability theory. A relationship is established between the mathematical formulation of different compatibility bifurcations and the canonical forms of catastrophe types. Examples of mechanisms demonstrating the existence of cuspoids of the compatibility conditions are given. An overall classification of the compatibility paths is also proposed.
LITERATURE REVIEW
Many structural systems can be described by introducing generalized coordinates. A great deal of work has been done in general nonlinear theory of elastic stability in terms of generalized coordinates (Thompson, 1963). A good summary of elastic stability is given by Thompson and Hunt (1973, 1984). In general, the relationship between the generalized coordinates and the load parameters of a structure is represented by equilibrium equations, which can be plotted resulting in equilibrium paths. Stability theory focuses on the study of critical points of these paths.
Figure 2.1 reproduces the four well-known modes of instability associated with distinct critical points in the coordinate system of a generalized coordinate ( Q ) and and a load parameter ( Λ ): the limit point, the asymmetric bifurcation, the stable symmetric bifurcation, and the unstable symmetric bifurcation. A comprehensive review article is given by Thompson (1969).
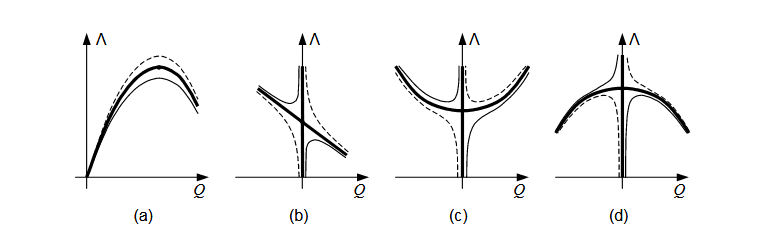
Figure 2.1: Equilibrium paths of structures with fundamental types of critical points (thick lines) and paths of the disturbed systems (thin lines). (a) Limit point. (b) Asymmetric bifurcation. (c) Stable symmetric bifurcation. (d) Unstable symmetric bifurcation
ANALOGY BETWEEN EQUILIBRIUM PATHS OF STRUCTURES AND COMPATIBILITY PATHS OF MECHANISMS
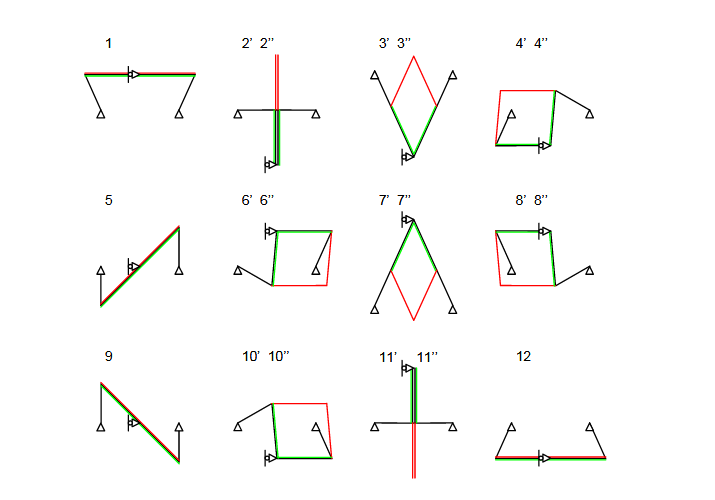
Figure 3.3: Characteristic configurations of the six-bar mechanism. Numbers correspond to those of positions
Characteristic points of the paths are marked by numbers and the corresponding configurations are shown in Figure 3.3. Bars AC and BC may have two different positions: they are drawn by dashed and dotted lines, also coloured red and green, respectively. The two configurations are referred to by single and double quotes following the number, respectively: 2 ′, 2 ′′, 3 ′, 3 ′′, 4 ′, 4 ′′, 6 ′, 6 ′′, 7 ′, 7 ′′, 8 ′, 8 ′′, 10 ′, 10 ′′, 11 ′ and 11 ′′. The chain ACB has only one position at points 1, 5, 9 and 12.
FURTHER STUDY OF COMPATIBILITY PATHS OF MECHANISMS
Various plots of compatibility paths have been shown so far in this dissertation. Due to the nonlinearity of the compatibility conditions, it is not always possible to obtain one kinematic state variable in terms of the other analytically.
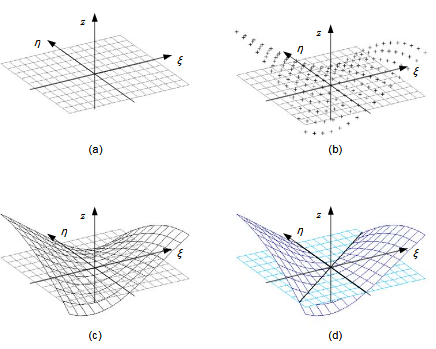
Figure 4.5: Numerical approximation of compatibility paths. (a) A rectangular grid is created on the state variable plane. (b) The compatibility condition is evaluated at the discrete grid points. (c) An approximate (linear) function is fitted to the values. (d) Zero positions are calculated
APPLICATION OF THE ELEMENTARY CATASTROPHE THEORY
In this chapter a new approach to the compatibility of mechanisms is presented. Firstly, it is summarized why the analysis previously shown might not always be sufficient. Secondly, elementary catastrophe theory is introduced followed by its applications in kinematics of mechanisms.
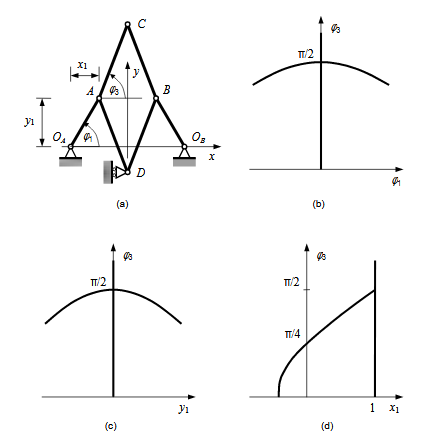
Figure 5.1 : A six-bar mechanism. (a) Basic structure. (b)-(d) Compatibility paths obtained using three different parameter sets
CONCLUSIONS
In this dissertation we have explored the relationship between the equilibrium of elastic structures and compatibility of mechanisms. The theory of elastic stability has a long history and a substantial amount of literature. Various instability phenomena have been studied in depth in the past. On the other hand, singularities of compatibility paths of mechanisms have attracted relatively little attention. We try to bridge this gap by establishing an analogy between the two subjects so that mathematical tools, used in structural stability, can be used in the analysis of compatibility of mechanisms.
FUTURE RESEARCH
A few questions may define the directions of future research in the subject as follows. This dissertation is primarily concerned with the existence and behaviour of singularities of compatibility paths of mechanisms. However, practical engineering design aims to avoid singularities which have an undesired effect on the design objectives. Examples demonstrated that the simple way of disturbing the system by small imperfections usually makes the bifurcation disappear. Though a sensible demand may arise to address the problem with a systematic approach and to develop appropriate design rules.
Furthermore, we have found the analytical formulation of the compatibility conditions became complicated as complex linkages were considered. Further study could be done on a more systematic way of writing the conditions. Numerical methods could be taken into consideration in order to develop an automated approach for the calculation of the system.
We have also encountered the more complicated situation where the increase of the instantaneous degrees-of-freedom at a singular point is more than one. In case of an increase of two, the corresponding equilibrium cases are the umbilic catastrophes whose equilibrium equations are derived from the potential function as a gradient vector. Consequently, the equations are related in a certain way that may not be valid for the compatibility conditions. It is to be the subject of further research whether compatibility can be formulated as a gradient system and how any classification can be carried out.
We have restricted our investigation to mechanisms with a single degree-of-freedom, which form a significant part of mechanical engineering research and design. However, 137 linkages can also be constructed with two or more degrees-of-freedom. The compatibility paths now are replaced by higher-dimensional manifolds. It is yet unexplored what relationship such systems may have with equilibrium of structures. The extension of the analogy into this direction requires a substantial amount of study.
Source: Oxford University
Author: András Lengyel
>> Civil Engineering Project Topics using Matlab for Final Year Students with Free Downloads
>> Huge List of Matlab Projects with Free Source Code