ABSTRACT
Excessive human-induced vibrations of assembly structures have been reported more frequently over the past two decades. In the automotive industry, the evaluation of the response of the human body to vibration is an important and active research area due to its significance in design safety. For example, the results of on-going research has led to the establishment of a number of models for predicting the effects of sitting posture, vibration magnitude and direction on the response of the human body when it is exposed to different types of vibration motion.
However, research focusing on structural engineering applications remains scarce, leading to inadequate design standards. For example, current structural design guidelines focus on human-induced vertical forces and assume linear structural behaviour, however, the most widely publicized problems have involved horizontal vibrations and many real-life structures are characterized by nonlinear behaviour. Following a brief investigation of vibration perception and comfort for subjects occupying a vibrating rig-structure, this dissertation focuses on human induced horizontal forces and examines the effect of nonlinear structural behaviour.
Dynamic horizontal loads of individuals performing predefined manoeuvres such as swaying and vertical jumping were measured in a laboratory setting. The fundamental force due to swaying occurred at the activity frequency. By contrast, the fundamental horizontal force due to vertical jumping did not always occur at the activity frequency. Furthermore, tests conducted for swaying were used to establish the relationship between the side-to-side force and the velocity of the subject‟s centre of mass. A customized foot switch system was also developed to monitor synchronization among individuals performing as a group in order to form a crowd loading model.
Models of analytic forces were derived based on measured data and used to evaluate structural response by focusing on a finite element model of a de-mountable grandstand characterized by nonlinear structural behaviour. The frequency spectra of displacement and acceleration responses showed clear peaks at the fundamental and the third harmonic of the swaying force, demonstrating the capability of the horizontal force to excite resonance. The resonant frequency decreased at higher levels of excitation, indicating a reduction in the stiffness due to the onset of nonlinear behaviour. Finally, load cases assuming synchronized and perfectly periodic group forces produced a significantly higher response compared to unsynchronized and imperfect group loads.
REVIEW OF THE LITERATURE
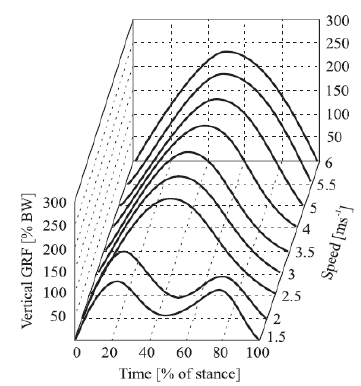
Figure 2.1: Typical profile of vertical forces during walking at different speeds after Keller et al
(1996) – the vertical axis shows the force as a percentage of body weight. The short horizontal axis shows the time as a percentage of the period when the foot is on the ground. About 30 years later, a study by Harper et al. (1961) reported comprehensive data for force measurements of individual footfalls during walking. Consideration of different speeds led to a more detailed model. The load-time history of a single footfall during walking was shown to have two peaks or single peak depending on the walking speed (see Figure 2.1 as an example).
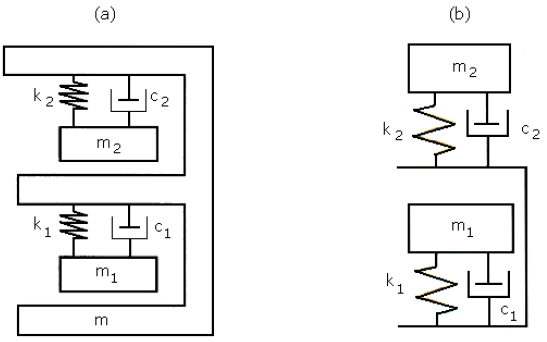
Figure 2.6: (a) Seated human model, (b) Standing human model
Sachse (2002) and Sim (2006) conducted separate investigations on the suitability of human body models found in biomechanics literature for structural engineering applications. Based on simplicity and good fit to experimental data, Sim (2006) concluded that the models proposed by Wei & Griffin (1998) and Matsumoto & Griffin (2003) were adequate for structural engineering applications. The seated and standing human models are shown in Figure 2.6a and b, respectively.
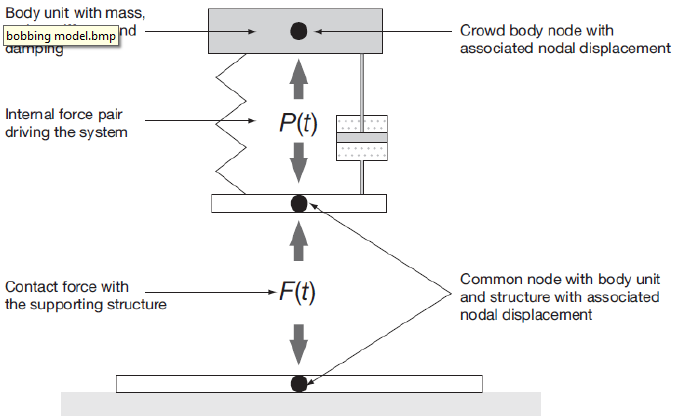
Figure 2.8: Model for the combined effect of active and passive humans on a structure (IStructE
2008)
Sim (2006) used a feedback model featuring the active and passive models she developed to represent the total effect. Another model based on a different approach was proposed by Dougill et al. 2006. Due to its simplicity and agreement with empirical data this model has been incorporated in the latest guidelines for dynamic assessment of permanent grandstands (see IStructE 2008). The model is illustrated in Figure 2.8 and the guidelines provide different parameters for this model for different design scenarios.
ASSESSMENT OF COMFORT LEVELS ON A VIBRATING GRANDSTAND RIG
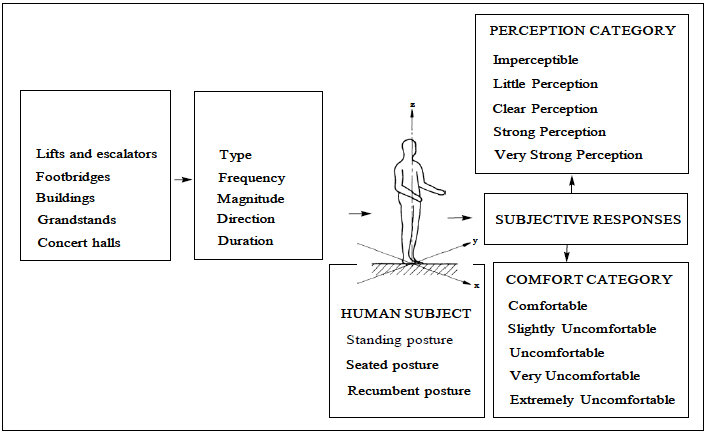
Figure 3.1 Flow chart of the category judgment method
Figure 3.1 shows the two categories of subjective responses or output that were requested from the participants after a brief period of exposure to a vibration input, namely, the level of vibration perception and the level of comfort together. The text descriptors shown in the flow chart are modified from BS6472 (1992). Five instead of the six descriptor used in BS6472 (1992) were adopted and the double negation form „not uncomfortable‟ was paraphrased to „comfortable‟.
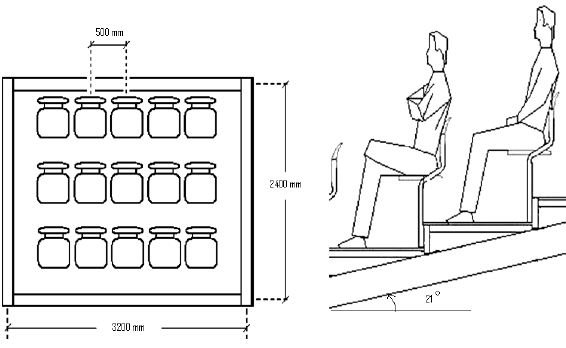
Figure 3.2: Overall geometry of grandstand rig (Comer et al. 2010)
The design of the rig is described in detail by Comer et al. (2007; 2010) and others. The essential features of the rig are that firstly, it was designed to resemble a real grandstand, including the raking; therefore human movement could be expected to be limited by the same spatial constraints of a normal grandstand structure (see Figure 3.2). Secondly, it could accommodate 15 individual subjects to allow group or crowd effects to be investigated.
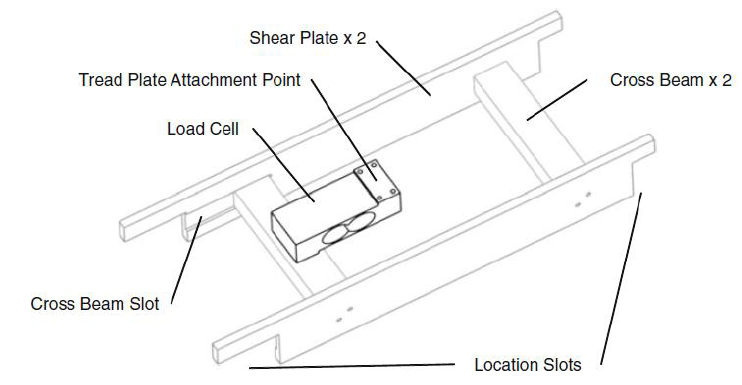
Figure 3.4: Load plate general assembly beneath the tread plate (Comer et al. 2010)
The rig was also instrumented with fifteen force plates to measure forces due to jumping and bobbing. These were positioned on the floor of the rig, in front of each seat. The force plates were fabricated from aluminium alloy and slotted between the cross beams which supported the seat rows (Figure 3.4).

Figure 3.18: Comparison of vertical force wave forms for subjects bobbing on a static deck (broken line) and bobbing at the same frequency but on a moving deck (solid line). Legend above (a) (b) (c) and (d) refer to Subject number – bobbing frequency in Hz/deck motion frequency in Hz/deck motion amplitude in mm
Changes in human-induced forces as a result of structural vibration were also observed when selected subjects were bobbing on a static deck compared with those obtained when the same subjects performed the same movement but on a vibrating deck (Figure 3.18). The vertical axis in Figure 3.18 shows the bobbing force normalized by subject weight.
HORIZONTAL FORCES AND MOTION GENERATED BY SWAYING AND JUMPING
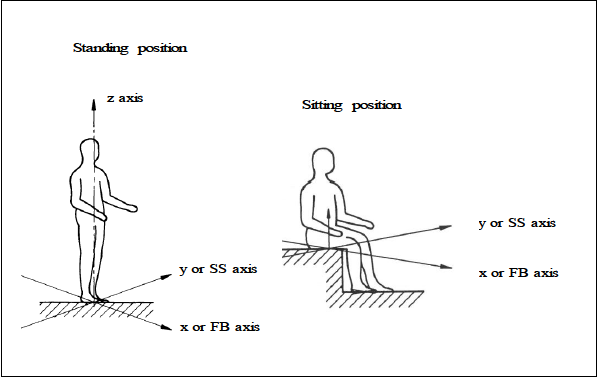
Figure 4.1e: Basicentric axis system used to describe the orientation of forces
In order to aid data interpretation, various analysis techniques were applied to the filtered data as discussed in the following sections. A notation system of axis was adopted to describe the direction of all horizontal forces as SS or FB for side-to-side and front-to-back forces, respectively. This is shown in Figure 4.1e relative to the x-y basicentric axis system used in BS7085.
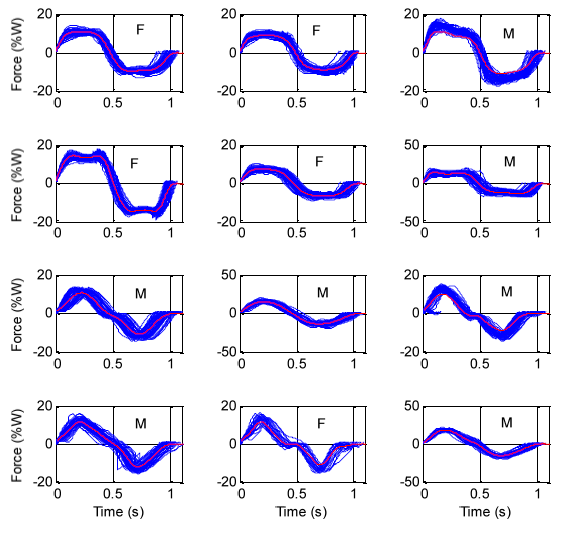
Figure 4.10: Force cycles separated to evaluate cycle durations (side-to-side standing sway)
Data describing the duration of each force cycle were obtained according to the same analysis procedure involving splitting a force record for each subject as discussed in Section 4.2.2.1. A typical example of force cycles used to evaluate the duration of each cycle is shown below (Figure 4.10) for all 12 male (M) and female (F) subjects.
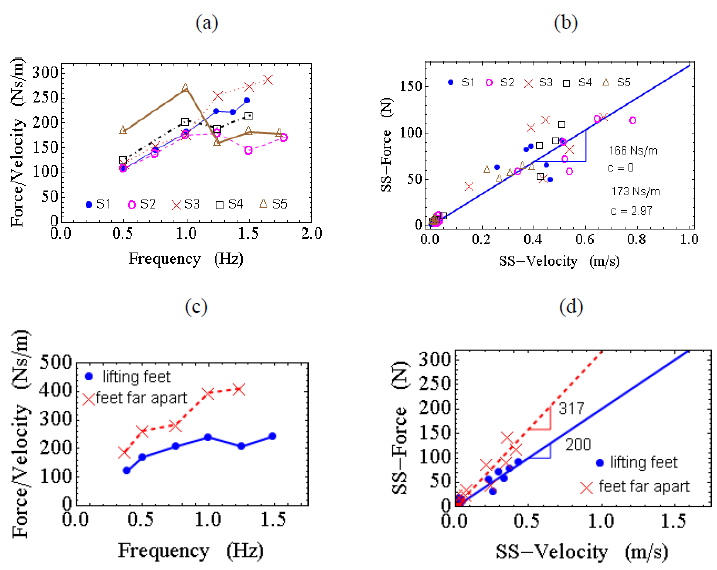
Figure 4.23: Parameter kcom evaluated for (a and b) five subjects, (c and d) different swaying conditions
Figure 4.23a shows a summary of results for the parameter kcom evaluated for all five subjects who participated in this category of tests. The dependence of kcom on the swaying frequency is evident even though there is inter-subject variability in the result. The force amplitude was also plotted against the velocity amplitude of the centre of mass for all frequencies considered (Figure 4.23b). There is a clear linearity of the data points which passes through the origin.
FOOTSWITCH DEVELOPMENT AND FOOT-TIMING MEASUREMENTS
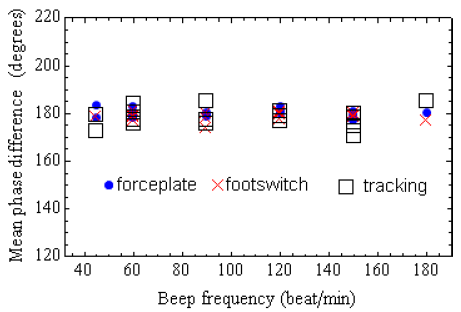
Figure 5.6: Mean phase difference between left and right foot
The mean phase differences between the right and left foot forces or landing recorded when one of the subjects was swaying at different beep frequencies are shown in Figure 5.6. As expected, all values recorded are close to 180 degrees. The values are slightly more or slightly less than 180 degrees because of the small overlapping region between the left foot landing and right foot take off during the double support phase.
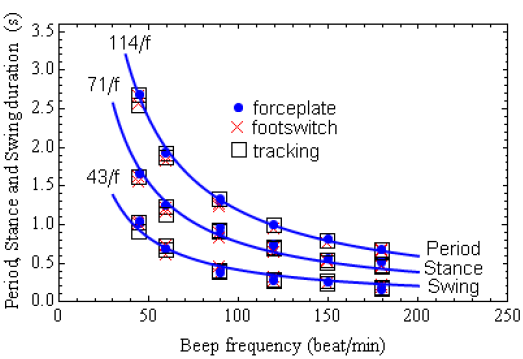
Figure 5.7: Period, Stance and Swing durations
Curves were fitted to each relevant data set to obtain analytic expressions for the period, stance and swing durations as a function of the beep frequency (f). These simple expressions are included in Figure 5.7 and can be used to interpolate values at the intermediate points where measurements were not made. It would be prudent to avoid extrapolation when using these curves.
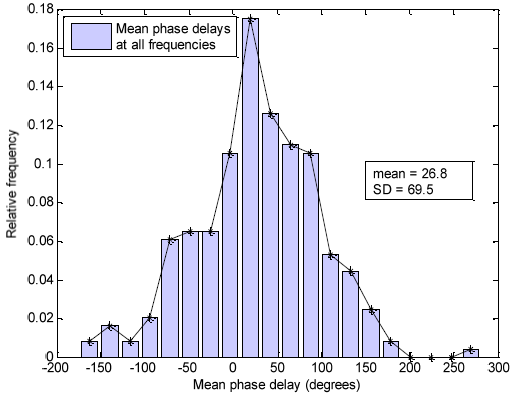
Figure 5.17: Histogram for mean phase delays for group-swaying – all frequencies
In the absence of evidence that mean phase delays are frequency dependent, the results for all frequencies were combined to form a large data set whose histogram distribution is shown in Figure 5.17. The histogram shows a peak around the mean indicating that there is a tendency for subjects to synchronize.
ANALYTICAL MODELLING OF HUMAN-INDUCED HORIZONTAL FORCES

Figure 6.2: Idealized (a) right and left rectangular force pulses for swaying side-to-side (b) Front and back rectangular force pulses for swaying front-to-back
Figure 6.1 relates to a rectangular pulse in one direction. However, for swaying, there is a pulse in each direction of swaying. Therefore, each right (HpR) or left (HpL) pulse of the split horizontal forces due to swaying side-to-side (HpF or HpB for swaying front-toback) can be represented schematically in the same time history as follows.
NUMERICAL PARAMETRIC STUDIES AND FINITE ELEMENT SIMULATIONS
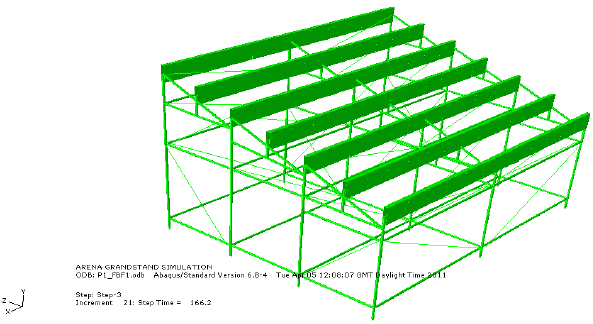
Figure 7.22: Finite element model
Gap elements were used to model the lack of fit in diagonal members (braces) including the lifting of the stand from some of its supports. The data from static tests suggested that the latter occurred when a horizontal load beyond a certain threshold caused an overturning effect when applied at the top of the stand. All structural members were modelled using beam elements with an average mesh length of 0.3 m as shown in Figure 7.22.
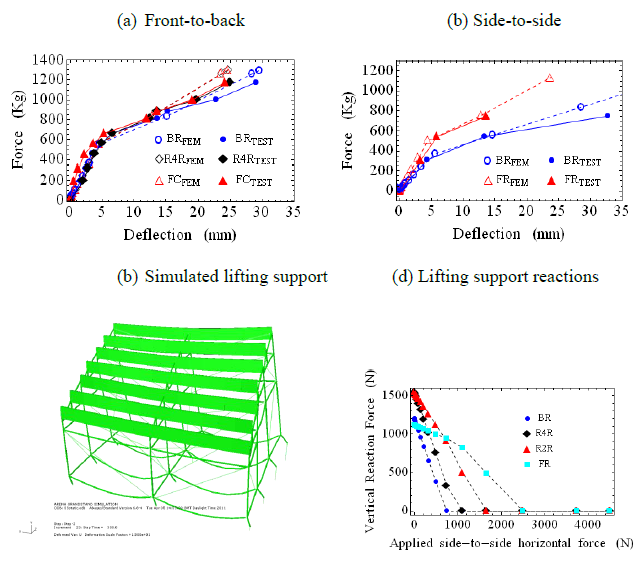
Figure 7.23: Static behaviour of stand and calibrated model
Figure 7.23 shows a comparison of measured and simulated static behaviour of the stand for this bracing pattern. The static tests involved pulling the deck of the stand by applying a horizontal force (side-to-side or front-to-back using a spreader beam to distribute the horizontal force) and measuring the resulting deflection at key locations on the deck. It is clear that the there was significant nonlinearity in the behaviour of the structure for large deflection amplitude.
CONCLUSIONS AND RECOMMENDATIONS FOR FUTURE WORK
Modern public structures are prone to excessive vibration levels induced by crowds. Whilst significant progress has been made in understanding the nature of this problem in the recent past, a review of literature highlighted a number of specific areas that required further research. The research presented in this thesis has focused on the following five areas.
- Human tolerance of vertical vibration motion when occupying a grandstand structure
- Measurement of human-induced horizontal forces generated by swaying and vertical jumping
- Footswitch based measurements of group synchronization during swaying
- Analytical modelling of human-induced horizontal forces
- Modelling the horizontal response of a demountable structure characterized by nonlinear behaviour
Tests were performed on an experimental grandstand rig in order to determine the threshold of perceptible and comfortable vibration levels for grandstand structures (Chapter 3). The test rig was moved at a known frequency and displacement. The test subjects were asked to score their perception and comfort state for each level of vibration. The acceleration limit at the onset of discomfort was found to be 5%g RMS. It was discovered that test subjects perceived the levels of vibration to be relatively high before they deemed it to be uncomfortable.
Source: Oxford University
Author: Sifiso Nhleko
>> Civil Engineering Project Topics using Matlab for Final Year Students with Free Downloads