ABSTRACT
Diabetes affects nearly 26 million Americans, according to the American Diabetes Association, with as many as three million Americans who have Type 1 Diabetes (ADA, 2015). Type 1 Diabetes (T1D) is autoimmune and characterized by little to no insulin production whereas Type 2 Diabetes (T2D) concerns insulin resistance and inability to use produced insulin.
Factors contributing to current diabetes management and regulation include exercise type, daily movement activities, and distinct tissue compartment metabolism, each challenging to model in a robust and comprehensive manner. Past models are highly limited in regard to exercise and varying glucose fluctuations dependent on type, intensity, and duration. Modeling could greatly enhance factors that contribute to diabetes management—currently, T1D is managed with a pump and/or injections, informed by constant blood glucose monitoring.
This thesis addresses knowledge gaps in the management and etiology of diabetes through development of a novel dynamic mathematical model informing controller design and implementation (artificial pancreas, continuous glucose monitors, and pumps). Diet and meal content on the basis of varying glycemic index and on the effects of activity and exercise, with lifestyle habit implications are a main focus. Emphasis is placed on model personalization with a T1D athlete example. The following model and case study implement specific aims:
- 10th order model designed in Matlab with 4 interrelated sub-models to integrate meal diversity, exercise activities, and personalized body composition.
- 3-State Glucose Compartmental Model o2-State Control Mechanisms: Insulin and Glucagon
- 2-State Digestion Model
- 2-State Exogenous Insulin Control o Skeletal Muscle Model with Mitochondrial State o Nonlinear relations including Hill Functions
- A 2 Phase Case Study, IRB approved for a Type 1 athletic 23-year-old female to evaluate and develop the model.
Results illustrate effects of meal type (slow vs. fast glycemic index) and exercise/activity based glucose-glycogen consumption on blood plasma glucose predictions and hormonal control action for both non-diabetic and diabetic model versions. Current challenges are addressed with model personalization, providing input flexibility for body mass, muscle ratio, stress, and types of diabetes (T1D, T2D) informing artificial pancreas design and possible sports performance applications.
BACKGROUND
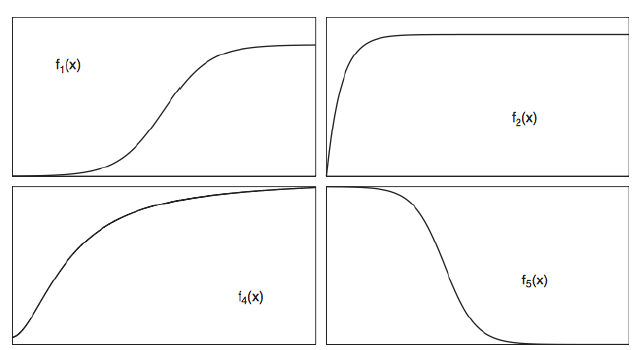
Figure 2.2: Li (2006) Function Shapes.
Figure 2.2: Li (2006) Function Shapes. Function shapes of respected states are plotted against BG concentration indicated by f1: insulin production simulated by glucose concentration, f2: insulindependent glucose consumers, dependent on BG alone, f4: insulin-dependent glucose uptake, and f5: glucose production controlled by insulin concentration (from Li, 2006).
Figure 2.3: Yamamoto (2014) Meal Simulation Model with Insulin. Left: Simulation of four staple foods with the proposed model compared to clinical data from Mohammed et al., 2004 (Yamamoto, 2014). Right: Simulation of subcutaneous insulin effect, as compared to clinical data used for Bergman model verification purposes (Yamamoto, 2014).
NOVEL MODELING APPROACH METHODOLOGY
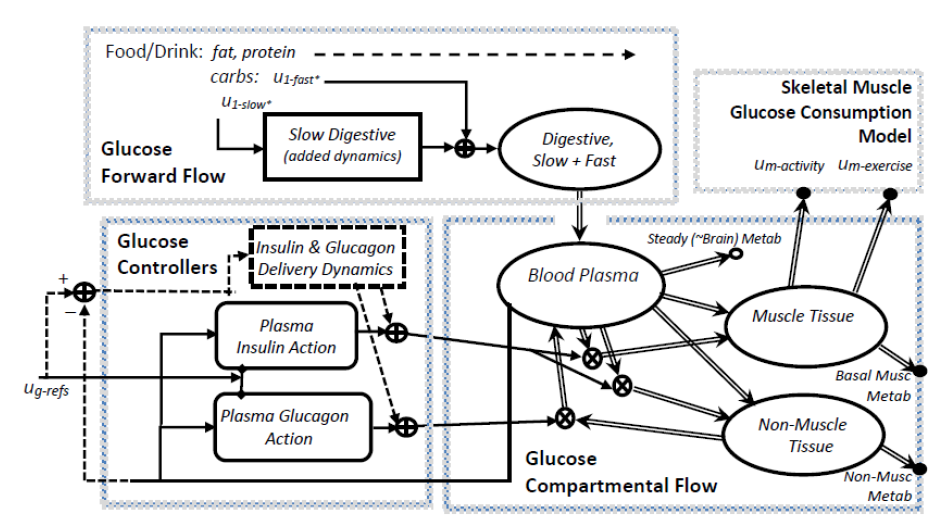
Figure 3.2: Schunk-Winters Compartmental Model Block Diagram and Structure.
Figure 3.2: Schunk-Winters Compartmental Model Block Diagram and Structure. Thick lines represent material flow with storage and control action as unidirectional signals informed by rate parameters and oftentimes, nonlinear, by either Hill kinetics or multiplicative states. Dashed lines represent exogenous control, via injection or other external device. Nonlinear relations include both flux terms and heuristics that change fitting equations based on different state or input signal ranges.
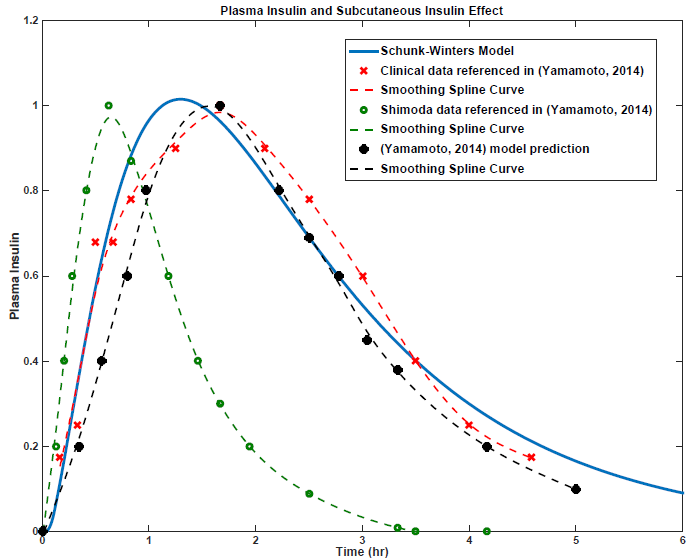
Figure 3.8: Insulin Submodel Validation and Literature Comparison.
Figure 3.8: Insulin Submodel Validation and Literature Comparison. Comparative insulin validation approach with a constant input amongst all sources of a fast-acting insulin bolus (i.e. Lispro in most studies) at t = 0 (1 time unit in the Schunk-Winters model for a duration of 5 time units, or 3 minutes) of 80 U/hr, or ~4 Units. Yamamoto and Shimoda plot subcutaneous insulin effect (min-1), or normalized so that the maximum peak is ‘1’. Clinical data is adapted from Swan (2009). All curves are adapted from picked data points of respective sources and fit using a smoothing spline function in Matlab.
Figure 3.16: Frequency of Most Sensitive Parameters. Frequency of most sensitive parameters using total appearances over all sensitivity trials. The most sensitive in regard to xg (Grefg, Greft, Kg2max, and Kg4max) are also shown as a frequency plot. Bias is eliminated toward foodstuff but only including meal and exercise simulations (snack is ignored). Top: Meal and exercise simulations combined (overall sensitivity without bias toward meals and/or exercise). Bottom: Xg state sensitivity for both meal and exercise combined.
PERSONALIZED ADAPTED MODEL FOR DIABETIC ATHLETES: IMPLEMENTATION OF A FEMALE TYPE 1 CASE STUDY
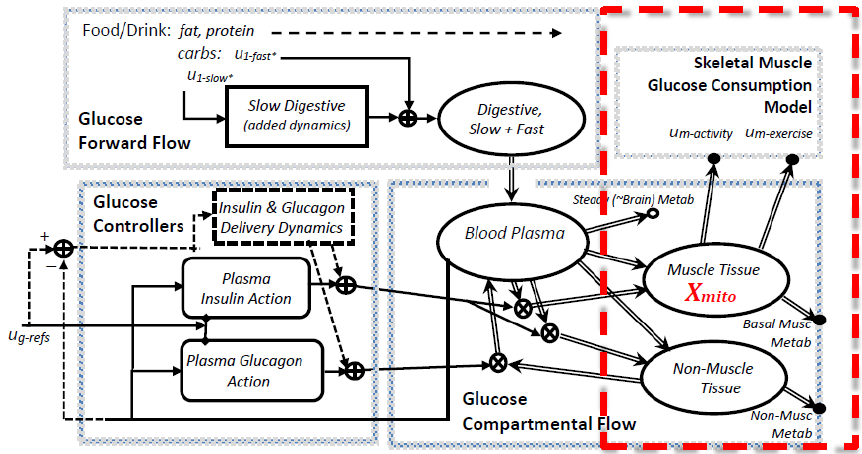
Figure 4.5: Schunk-Winters Model Structure with Exercise Focus.
Figure 4.5: Schunk-Winters Model Structure with Exercise Focus. Thick lines represent material flow with storage and control action as unidirectional signals informed by rate parameters and oftentimes, nonlinear, by either Hill kinetics or multiplicative states. Nonlinear relations include both flux terms and heuristics that change fitting equations based on different state or input signal ranges.
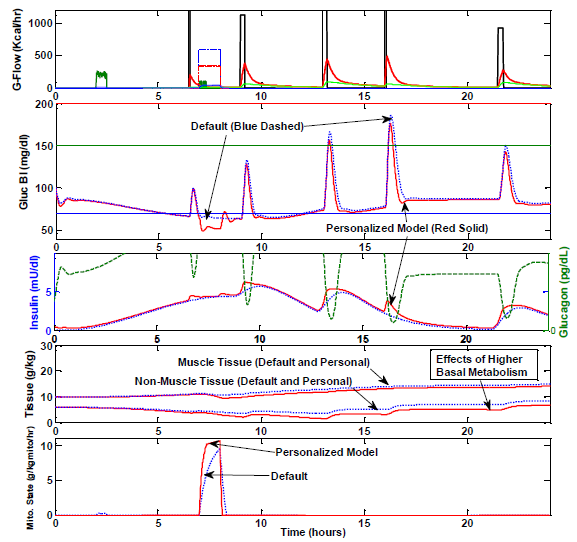
Figure 4.15: Comparison of Default and Personalized Model. Case study day 5 (Sprint Training) using default vs. personalized parameters described.
These values were decided after analyzing case study results; however, were presented in 4.3.2 to outline parameters used for model simulations throughout Section 4.4. Figure 4.15 shows a model comparison by overplot of the new, personalized model for the case study subject compared to the prediction using only default values.
CONCLUSION AND FUTURE DIRECTIONS
Chapter 3, the general Schunk-Winters model, is intended for both research and clinical use, particularly diabetes educators, and to develop medical device technologies in order to eliminate guesswork of bolus corrections, often in error due to unknown food GI or exercise effects. This may help people with diabetes manage BG with exercise, diet, and dual-hormonal control based on algorithm feedback. Chapter 3 provides a model that can take a wider variety of lifestyle inputs than most CGM and artificial pancreas designs, enhancing where BG is headed before it occurs.
For example, a device working under the Schunk-Winters default model would inform a person eating a 50g low GI meal vs. a 50g high GI meal differently, and furthermore make different predictions based on different consumption times for the same meal content. It can then be used to inform a person or an artificial pancreas algorithm to adjust any insulin bolus given—other models do not do this and hypoglycemia may occur in the low GI and slow consumption case, if the same insulin amount is taken for both high and low GI of the same CHO amount.
As discussed in Section 3.4.7, additional hormonal controllers may provide increased control in addition to strictly glucagon and insulin. Oftentimes, gradients of glucose to blood plasma exist, without means of foodstuff ingestion, etc. Additional hormone control could be categorized into 3 cases: 1) real-time rate controlling for both digestive rates (i.e. slow path) and glucagon tissue effects during periods of high BG, in particular slowing down glucose delivery fluxes (operating somewhat in tandem with insulin, e.g. similar to the role of amylin hormone), 2) real-time ‘anticipatory’ for sympathetic nervous system “stress” effects, and 3) longer-term adaptive adjustments for energy storage.
Source: Marquette University
Authors: Sofie Schunk
>> 200+ Matlab Projects based on Control System for Final Year Students

